A parte da mecânica que estuda a descrição dos movimentos é chamada de cinemática e aquela que estuda as causas dos movimentos, de dinâmica.
Partícula ou Ponto Material é o tipo de corpo mais simples que pode-se imaginar. Possui dimensões desprezíveis, é um corpo que em situações específicas pode ser considerado como um ponto no espaço.
Um Sistema Físico é qualquer parte do universo bem definida.
Um Sistema de Partículas é um conjunto de partículas que forma um sistema físico.
um corpo rígido é um conjunto de partículas cuja distância entre qualquer par de partículas do conjunto permanece sempre a mesma.
Um Sistema Rígido é um sistema qualquer de partículas cuja distância entre qualquer par de suas partículas permanece sempre a mesma.
A reta na qual foram específicadas a origem, os semi-eixos positivo e negativo e a correspondência entre pontos e números é chamada de um Eixo Coordenado.
Um Sistema de Coordenadas é caracterizado por três eixos coordenados OX, OY e OZ, ortogonais entre si e com origem comum O.
play_circle_filledDizemos que a trinca de coordenadas dá a Posição da partícula em relação a OXYZ.
Um Referencial é uma estrutura para medir posições e instantes de tempo e é formado por um sistema de coordenadas, junto com as réguas e os relógios.
Um Observador é um agente fixo em um referencial e é capaz de realizar medições. O observador pode ser uma pessoa ou um aparelho programado para medir. É conveniente supor que os relógios estão sincronizados em um dado referencial para que haja um único instante do tempo atribuido a um dado evento.
Dizemos que uma partícula está em Movimento em relação a um referencial quando sua posição em relação ao referencial muda com o passar do tempo.
Partícula em Movimento 1D
Podemos considerar qualquer eixo coordenado para representar um movimento em uma dimensão (Movimento 1D). Para facilitar nosso estudo, iremos representar a posição da uma partícula que se move na direção x pela notação
Deslocamento é a diferença entre a posição final da partícula e a posição inicial da partícula.
Como sabemos, na Física existem dois tipos de grandezas, as Grandezas Escalares que são representadas apenas por um número, ou valor numérico e as Grandezas Vetoriais que são representadas por um módulo (valor numérico), uma direção e um sentido.
O deslocamento é uma grandeza vetorial, Δx indica o módulo e a direção, enquanto que o sinal irá indicar o sentido. O mesmo vale para Δy e Δz.
A Velocidade Média é a razão entre o deslocamento e o intervalo de tempo decorrido.
No Sistema Internacional de Unidades e Medidas (SI) o espaço é medido em metros (m) e o tempo é medido em segundos (s) , logo a velocidade será dada em metros por segundo (m/s).
A Velocidade Instantânea é definida como o limite da razão Δx/Δt da partícula quando o tempo tende a zero, ou ainda, é a derivada da posição da partícula em relação ao tempo. Determina a mudança do espaço conforme passa o tempo.
ou
A Aceleração média é a razão entre a variação da velocidade e o tempo decorrido.
No Sistema Internacional de Unidades e Medidas (SI) o espaço é medido em metros (m) e o tempo é medido em segundos (s) , a velocidade dada em metros por segundo (m/s) e a aceleração será dada em metros por segundo ao quadrado (m/s²).
A Aceleração Instantânea é definida como o limite da razão Δv/Δt da partícula quando o tempo tende a zero, ou ainda, é a derivada da velocidade da partícula em relação ao tempo. Determina a mudança da velocidade conforme passa o tempo.
ou
Movimento Retilíneo Uniforme – MRU
Temos um MRU quando a velocidade da partícula é constante e sua aceleração é nula. Como o nome informa, a partícula não executa movimentos curvilíneos. É o movimento mais somples de todos.
A Função de Movimento da partícula em MRU é a regra que descreve a posição da partícula em cada instante de tempo.
Onde é a posição inicial,
é a velocidade da partícula e
é o instante de tempo.
APLICAÇÃO
Exemplo 1.1 – Vamos considerar uma partícula cujo movimento é descrito pela função de movimento dada por
onde a posição é dada em metros (m) e o tempo em segundos (s). Quais são (a) a posição da partícula, (b) a velocidade e (c) a aceleração em t = 3s?
Como vemos, a partícula está na posição x = 17m quando t = 3s;
Para calcularmos a velocidade neste instante, tomemos a função
Como vemos, a velocidade da partícula é constante e igual a v = 5 m/s, desta forma a aceleração é nula.
Resolução de Exercício – 01
play_circle_filledMovimento Retilíneo Uniformemente Variado – MRUV
Considere agora o movimento retilíneo no qual a velocidade varia uniformemente com o tempo, em outras palavras, a aceleração da partícula é constante.
A equação acima é obtida tomando-se o intante de tempo inicial igual a zero e o instante de tempo final igual a im instante qualquer. Esta equação é conhecida como a função horária da velocidade para o MRUV.
A função de movimento da partícula em MRUV é dada por
A equação de Torricelli é obtida combinando-se as funções horárias da posição e da velocidade e não é dependente do tempo.
APLICAÇÃO
Exemplo 1.2 – Vamos considerar uma partícula cujo movimento é descrito pela função de movimento dada por
onde a posição é dada em metros (m) e o tempo em segundos (s). Quais são (a) a posição da partícula, (b) a velocidade e (c) a aceleração em t = 3s?
Como vemos, a partícula está na posição x = 47m quando t = 3s;
Para calcularmos a velocidade neste instante, tomemos a função
Temos que a velocidade da partícula no instante t = 3s é de v = 30 m/s.
A velocidade para um instante qualquer é dada por
Podemos usar o mesmo procedimento para calcularmos a aceleração instantânea.
Neste caso a aceleração é constante e igual a 10 m/s².
Resolução de Exercício – 02
play_circle_filledResolução de Exercício – 03
play_circle_filledResolução de Exercício – 04
play_circle_filledMovimento 1D – Formulação Geral
É importante escrevermos as denifições das grandezas da cinemática na formulação que utiliza os conceitos de derivação e integração.
Em um sistema em que o objeto, ou partícula, está se movendo em uma dimensão, podemos definir a aceleração instantânea pela forma descrita abaixo:
Podemos reescrever a equação acima na forma da integração, que é a operação inversa à derivação,
O mesmo vale para a definição de velocidade, temos
Logo, reescrevendo na forma integral
Para resolvermos a derivada de um monômio, temos que, se m e n são números reais, temos que
e para resolvermos a integral de um monômio, basta realizar as operaçães inversas, assim
A área algébrica sob o gráfico de uma função qualquer em um certo intervalo do domínio e igual à integral da função nesse intervalo.
APLICAÇÃO
Exemplo 1.2 – Considere duas partícula, A e B, se movimentando em linha reta pelo eixo OX, com funções horárias dadas por
Note que, sabemos a função horária da posição para a partícula A e a função horária da aceleração para a partícula B. Queremos encontrar as funções x(t), v(t) e a(t) para ambas as partícula. Iniciaremos com a partícula A, logo
a derivada de uma constante é zero. A velocidade varia linearmente com o tempo.
Calculando-se a aceleração da partícula A, tem-se
a aceleração é constante. Note que não estamos utilizando um sistema de unidades. Assim,
Para a partícula B, temos
Neste caso, a velocidade e o tempo iniciais são nulos.
Para determinarmos a função que descreve a posição da partícula, temos
a posição e o tempo iniciais são nulos. Portanto,
Resolução de Exercício – 04
play_circle_filledResolução de Exercício – 05
play_circle_filledMovimento de Queda Livre
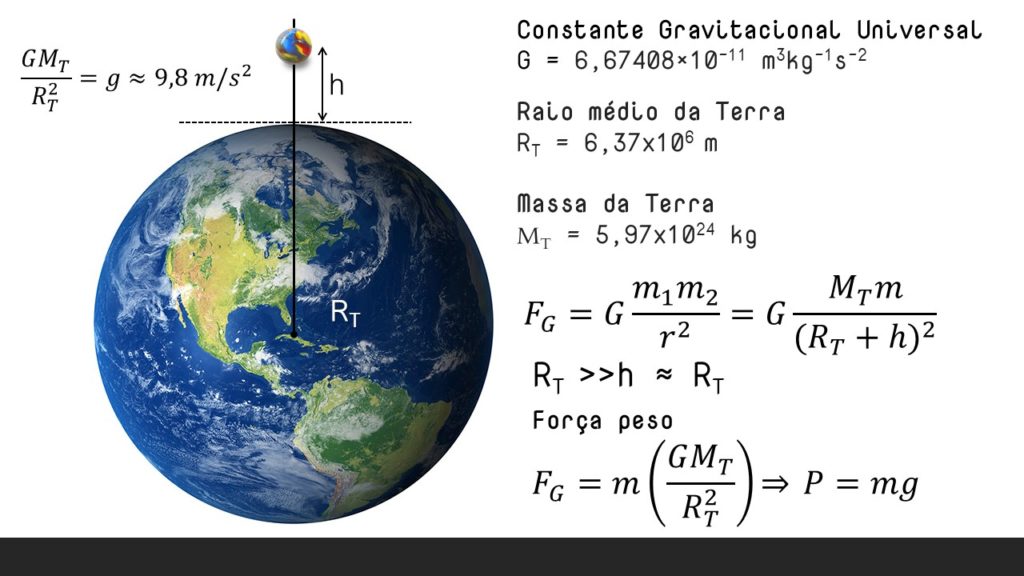
De uma forma genérica, dizemos que um corpo está executando um movimento de queda livre se o seu movimento for vertical, isto é, se tiver a direção que passe pelo centro da Terra, e se não sofrer nenhuma ação que não seja a da força gravitacional da Terra.
O Movimento de queda livre é uma aplicação do Movimento Retilíneo Uniformemente Variado, pois a aceleração da partícula é aproximadamente constante e igual a
As equações do movimento de queda livre são dadas pelas equações do MRUV, também são válidas para o chamado movimento vertical, que são
Resolução de Exercício – 06
play_circle_filledResolução de Exercício – 07
play_circle_filledResolução de Exercício – 08
play_circle_filledObrigado e bons estudos!
BIBLIOGRAFIA
HIBBELER, R. C. Dinâmica: Mecânica para Engenharia. Edição: 12 ed. São Paulo (SP): Pearson Universidades, 2010.
NUSSENZVEIG, H. M. Curso de Física Básica: Mecânica. Edição: 5 ed. [s.l.] Blucher, 2013.
RESNICK, R.; WALKER, J.; HALLIDAY, D. Fundamentos de Física – Volume 1 – Mecânica. Edição: 10 ed. [s.l.] LTC, 2016.
SERWAY, R.; JEWETT, J. Princípios de física – vol. I: Volume 1. Edição: 2 ed. [s.l.] Cengage Learning, 2014.
YOUNG, H. D.; FREEDMAN, R. A. Física de Sears & Zemansky: Volume I: Mecânica: Volume 1. Edição: 14 ed. [s.l.] Pearson Universidades, 2015.