Movimentos 2D e 3D

Consideremos que a partícula pode executar um movimento qualquer no espaço, desta forma teremos uma grande possibilidade de movimentos. Neste capítulo iremos estudar os movimento 2D e 3D, retilíneos e curvilíneos.

Incluiremos o conceito de vetor de forma natural e intuitiva, inicialmente, para que possamos desenvolver este conceito ao longo do curso.

Como sabemos, um vetor é uma entidade matemática que é representada geometricamente no espaço por meio de um módulo (tamanho), uma direção e um sentido, o que lhe possibilita ser um segmento de reta orientado.

Se considerarmos um vetor , dizemos que este vetor é determinado pelo segmento de reta AB de origem em A e extremidade em B.

Vetor Posição é o vetor que localiza a partícula em relação ao referencial, marco zero. Podemos defini-lo como sendo

\vec{r}=x \hat{i}+y \hat{j}+ z \hat{k}

Os vetores , são os vetores unitários relacionados aos eixos coordenados e formam a base do espaço vetorial. Toda grandeza física vetorial pode ser representada por uma soma destes vetores canônicos.

Vetor Velocidade é o vetor que informa como o vetor posição está variando ao longo do tempo. Podemos defini-lo como sendo

\vec{v}=\frac{d \vec{r}}{dt}=\frac{dx}{dt} \hat{i}+\frac{dy}{dt}\hat{j}+\frac{dz}{dt} \hat{k}

\vec{v}=v_{x} \hat{i}+v_{y} \hat{j}+v_{z} \hat{k}

A velocidade vetorial instantânea da partícula, tem a direção da reta tangente à trajetória no ponto onde se encontra a partícula nesse instante.

Vetor Aceleração é o vetor que informa como o vetor velocidade está variando ao longo do tempo. Podemos defini-lo como sendo

\vec{a}=\frac{d \vec{v}}{dt}=\frac{dv_{x}}{dt} \hat{i}+\frac{d v_{y}}{dt}\hat{j}+\frac{d v_{z}}{dt} \hat{k}

\vec{a}=a_{x} \hat{i}+a_{y} \hat{j}+a_{z} \hat{k}

Qualquer que seja a direção da aceleração instantânea, o seu sentido jamais aponta para fora da concavidade da trajetória.

Podemos ainda, definir o vetor Deslocamento

\Delta \vec{r}=\vec{r_{f}}-\vec{r_{i}}

\Delta \vec{r}=\left ( x_{f} \hat{i}+y_{f} \hat{j}+ z_{f} \hat{k} \right)-\left ( x_{i} \hat{i}+y_{i} \hat{j}+ z_{i} \hat{k}  \right)

\Delta \vec{r}=\left ( x_{f}-x_{i} \right) \hat{i}+\left ( y_{f}-y_{i} \right) \hat{j}+\left ( z_{f}-z_{i} \right) \hat{k}

\Delta \vec{r}=\Delta x \hat{i}+ \Delta y \hat{j}+ \Delta z \hat{k}

O Vetor Velocidade Média

\vec{v}_{m}=\frac{\Delta \vec{r}}{\Delta t}

\vec{v}_{m}=\frac{\Delta x}{\Delta t} \hat{i}+ \frac{\Delta y}{\Delta t} \hat{j}+ \frac{\Delta z}{\Delta t} \hat{k}

O Vetor Aceleração Média

\vec{a}_{m}=\frac{\Delta \vec{v}}{\Delta t}

\vec{a}_{m}=\frac{\Delta v_{x}}{\Delta t} \hat{i}+ \frac{\Delta v_{y}}{\Delta t} \hat{j}+ \frac{\Delta v_{z}}{\Delta t} \hat{k}

Movimento 2D – Lançamento de Projéteis

Quando uma partícula se movimenta em um plano e apresenta uma velocidade com componentes vertical e horizontal, o movimento é dito 2D.

Os casos particulares do movimento 2D são o Lançamento Oblíquo e o Lançamento Horizontal

Sabe-se que estes movimentos são uma combinação dos movimento MRU e MRUV, de forma que, na direção x do movimento a velocidade a constante e na direção y do movimento a partícula é acelerada, g = 9,8 m/s². Todas as forças de resistência e de arrasto são desprezadas.

As equações que descrevem o movimento são, para o eixo y (MRUV)

\begin{cases}
  y_{f}=y_{i}+v_{yi}t-\frac{1}{2}gt^2 \\ 
  v_{f}=v_{i}-gt \\ 
  v_{f}^{2}=v_{i}^{2}-2g \Delta y
\end{cases}

para o eixo x (MRU)

\{x_{f}=x_{i}-v_{xi}t

As componentes da velocidade inicial da partícula são dadas por

\begin{cases}
v_{xi}=v_{i}  cos \theta \\ 
v_{yi}=v_{i} sen  \theta \\
\end{cases}

Combinando-se as equações da posição, encontra-se a equação da trajetória da partícula, logo

y_{f}=y_{i}+ \frac{v_{yi}}{v_{xi}} \Delta x -\frac{g}{2} \left( \frac{\Delta x}{v_{xi}} \right)^{2}

Forma alternativa, utilizando-se o ângulo de lançamento

y_{f}=y_{i}+ \tan \theta \Delta x -\frac{g}{2v_{i}^{2}} \left( \tan^{2} \theta +1\right) \Delta x^{2}

Define-se o Alcance R como sendo a distância horizontal do ponto inicial do lançamento ao ponto final do lançamento.

R=x_{i}+\frac{v_{i}cos \theta}{g} \left( v_{i}sen \theta+\sqrt{v_{i}^{2}sen^2 \theta+2y_{i}g} \right)

Define-se a Altura Máxima H como sendo a distância vertical do ponto de lançamento ao ponto máximo da posição ao longo do eixo vertical.

H=y_{i}+\frac{v_{i}^{2}sen^2 \theta}{2g}

Para o caso particular em que a partícula é lançada da origem do sistema de referência, temos

\begin{cases}
  y= \tan \theta x -\frac{gx^2}{2v_{i}^{2}} \left( \tan^{2} \theta +1\right) \\ 
  R=\frac{v_{i}^{2}sen(2 \theta)}{g} \\ 
  H= \frac{v_{i}^{2}sen^2 \theta}{2g} 
\end{cases}

Note que o alcance máximo ocorre quando o seno adquire o maior valor que é 1, logo, pela equação do alcance θ = 45°.

Noções sobre vetores

Aplicações de Lançamento Oblíquo

Movimento Circular

O Movimento Circular é um exemplo de movimento em um plano, Movimento 2D, cuja trajetória da partícula é definida pela equação

x^2+y^2=r^2

onde, x e y são as coordenadas da partícula no plano xy e r é o raio da trajetória circular.

Podemos escrever esta equação em coordenadas polares considerando que

\begin{cases}
x=rcos \theta \\
y=rsen \theta
\end{cases}

onde θ é a coordenada angular da partícula.

As coordenadas e os vetores de base para as coordenadas cartesianas e as coordenadas polares são, respectivamente

\begin{cases}
(x,y) \rightarrow  \left\{ \hat{i}, \hat{j} \right\}      \\
(r, \theta) \rightarrow  \left\{ \hat{r}, \hat{\theta} \right\}
\end{cases}

Temos que, é o vetor unitárito radial e é o vetor unitário tangencial à trajetória circular.

Podemos determinar forma da de cada vetor de base em coordenadas polares como função dos vetores de base das coordenadas cartesianas, para isso devemos calcular a forma do vetor posição da partícula em movimento circular, assim

Vetor Posição em Coordenadas Polares

\vec{r}=x \hat{i}+y \hat{j} \\
\vec{r}=rcos \theta \hat{i}+rsen \theta \hat{j} \\
\vec{r}=r(cos \theta \hat{i}+sen \theta \hat{j}) \\

Definindo o vetor unitário radial

\hat{r}=cos \theta \hat{i}+sen \theta \hat{j}

logo,

\vec{r}=r \hat{r} 

Podemos definir a grandeza velocidade angular média como

\omega_m =\frac{\theta_f - \theta_i}{t_f - t_i}=\frac{\Delta \theta}{\Delta t}

no SI a unidade física desta grandeza é rad/s.

A velocidade angular instantânea é definida por

\omega = \lim_{\Delta t \rightarrow 0}\frac{\Delta \theta}{\Delta t}=\frac{d \theta}{dt}

Caso a velocidade angular mude com o tempo, a grandeza que mede a forma como a velocidade angular altera é a aceleração angular.

A aceleração angular média é definida por

\alpha_m =\frac{\omega_f - \omega_i}{t_f - t_i}=\frac{\Delta \omega}{\Delta t}

no SI a unidade física desta grandeza é rad/s².

A aceleração angular instantânea α é definida por

\alpha = \lim_{\Delta t \rightarrow 0}\frac{\Delta \omega}{\Delta t}=\frac{d \omega}{dt}

Podemos determinar o vetor velocidade da partícula derivando-se o vetor posição em relação ao tempo

\vec{v}=\frac{d \vec{r}}{dt}=\frac{d}{dt}(r \hat{r})

Utilizando-se a regra da cadeia

\vec{v}=\frac{dr}{dt} \hat{r}+ r \frac{d \hat{r}}{dt}

como o raio da trajetória circular é constante a derivada do raio em relação ao tempo é nula, assim

\vec{v}=r \frac{d \hat{r}}{dt}=r \frac{d}{dt}(cos \theta \hat{i}+sen \theta \hat{j})

\vec{v}=r \left(  \frac{d}{dt}cos \theta \hat{i}+\frac{d}{dt} sen \theta \hat{j} \right)

\vec{v}=r \left( -sen \theta \frac{d \theta}{dt} \hat{i}+cos \theta \frac{d \theta}{dt} \hat{j} \right)

\vec{v}=r \omega \left( -sen \theta \hat{i} + cos \theta \hat{j}\right)

Definindo o vetor unitário tangencial

\hat{\theta}=-sen \theta \hat{i}+cos \theta \hat{j}

logo, o vetor velocidade da partícula fica

\vec{v}=r \omega \hat{\theta}

Podemos determinar a aceleração da partícula derivando-se a velocidade em relação ao tempo

\vec{a}=\frac{d \vec{v}}{dt}=\frac{d}{dt}(r \omega \hat{\theta})

Sabe-se que o raio da trajetória é constante e aplicando-se a regra da cadeia

\vec{a}=r \left( \frac{d \omega}{dt} \hat{\theta}+\omega \frac{d \hat{\theta}}{dt} \right)

o termo que precisamos derivar é

\frac{d \hat{\theta}}{dt}=\frac{d}{dt}\left( -sen \theta \hat{i} + cos \theta \hat{j} \right)

\frac{d \hat{\theta}}{dt}= -cos \theta \frac{d \theta}{dt} \hat{i} - sen \theta \frac{d \theta}{dt} \hat{j}

\frac{d \hat{\theta}}{dt}=-\omega \left( cos \theta \hat{i} + sen \theta \hat{j} \right)

\frac{d \hat{\theta}}{dt}=-\omega \hat{r}

O vetor aceleração da partícula fica

\vec{a}=r \alpha \hat{\theta}-r\omega^{2}\hat{r}

Vemos que a aceleração radial aponta para o centro da trajetória, é chamada de aceleração centrípeta.

Neste ponto podemos fazer uma análise do movimento circular classificando-o como MCU e MCUV.

Movimento Circular Uniforme – MCU

As características deste movimento são

\begin{cases}
r\equiv  constante \\
\omega \equiv constante \\
\alpha = 0 \\
v=r \omega \\
a_c=r \omega^{2}=\frac{v^2}{r} \\
\theta_{f}=\theta_{i}+ \omega t
\end{cases}

O MCU é um movimento acelerado.

Movimento Circular Uniformemente Variado – MCUV

As características deste movimento são

\begin{cases}
r\equiv  constante \\
\alpha \equiv constante \\
v=r \omega \\
a_c=r \omega^{2}=\frac{v^2}{r} \\
a_t=r \alpha \\
\theta_{f}=\theta_{i}+ \omega_{i} t + \frac{1}{2} \alpha t^2 \\
\omega_{f}=\omega_{i}+\alpha t \\
\omega_{f}^{2}=\omega_{i}^{2}+2\alpha \Delta \theta
\end{cases}

Exercícios

Em uma estrada, dois carros, A e B, entram simultaneamente em curvas paralelas, com raios $R_A$ e $R_B$. Os velocímetros de ambos os carros indicam, ao longo de todo o trecho curvo, valores constantes $v_A$ e $v_B$. Se os carros saem das curvas ao mesmo tempo, qual é a relação entre $v_A$ e $v_B$.

Num plano horizontal sem atrito, uma partícula $m_1$ move-se com movimento circular uniforme e raio R e velocidade angular $\omega$. Ao passar pelo ponto P, outra partícula, $m_2$, é lançada do ponto O com velocidade $v_0$. Qual o valor de $v_0$ para que $m_1$e $m_2$ colidam em Q?

Quando se dá uma pedalada na bicicleta ao lado (isto é, quando a coroa acionada pelos pedais dá uma volta completa), qual é a distância aproximada percorrida pela bicicleta, sabendo-se que o comprimento de um círculo de raio R é igual a $2\pi R$, onde $\pi = 3$?

Fazendo parte da tecnologia hospitalar, o aparelho representado na figura é capaz de controlar a administração de medicamentos em um paciente. Regulando-se o aparelho para girar com frequência de 0,25 Hz, pequenos roletes das pontas da estrela, distantes 6 cm do centro desta, esmagam a mangueira flexível contra um anteparo curvo e rígido, fazendo com que o líquido seja obrigado a se mover em direção ao gotejador. Sob essas condições, a velocidade escalar média imposta ao líquido em uma volta completa da estrela é, em m/s, Dado: $\pi = 3,1$

A figura abaixo mostra um sistema de engrenagem com três discos acoplados, cada um girando em torno de um eixo fixo. Os dentes dos discos são do mesmo tamanho e o número deles ao longo de sua
circunferência é o seguinte: X = 30 dentes, Y = 10 dentes, Z = 40 dentes. Se o disco X dá 12 voltas, quantas voltas dará o disco Z?

Movimento Curvilíneo

Para o caso em que a trajetória curvilínea for expressa por y=f(x), e o raio de curvatura ρ em qualquer ponto sobre a trajetória é determinado pela equação

\rho=\frac{\left[ 1+ \frac{dy}{dx}^{2} \right]^{3/2}}{\left| \frac{d^2y}{dx^2} \right| }

As características deste movimento são

\begin{cases}
\vec{v}=\frac{dr}{dt}\hat{\theta} \\
\vec{a}=a_t\hat{\theta}+\frac{v^2}{\rho}\hat{r} \\
a=\sqrt{a_t^{2}+\frac{v^4}{\rho^2}}
\end{cases}

A velocidade da partícula é sempre tengente à trajetória e a componente radial da aceleração é o resultado da taxa de variação temporal da velocidade. Esta componente está sempre direcionada para o centro de curvatura da trajetória.

Movimento Relativo

Tomemos o exemplo onde um marinheiro ao lado da base do mastro de um navio lança uma bola de canhão para cima, tentando alcançar o topo do mastro. Ele vê a bola subindo, alcançando o topo do mastro e caindo em linha reta até sua posição, mesmo se o navio estiver em movimento retilíneo uniforme. No entanto, para um segundo marinheiro parado observando da margem do rio o navio em movimento, a trajetória da bola de canhão é parabólica.

As descrições cinemáticas que os dois observadores fornecem do movimento do projétil são diferentes, mas as descrições dinâmicas são coincidentes: eles medem aceleração nula para o movimento horizontal do projétil (), mesma aceleração na direção vertical () , mesmo tempo do movimento.

O princípio da relatividade diz que, afim de que a natureza, a Física, tenha o mesmo comportamento quando experimentada ou descrita por diferentes observadores inerciais, é necessário que as equações da física tenham a mesma forma matemática em todos os referenciais inerciais, a mesma estrutura de dependência entre as grandezas fisicamente relevantes.

Consideremos a figura a seguir, tem-se dois referenciais inerciais, com o referencial A em repouso e o referencial B em movimento retilíneo uniforme, definindo os vetores como

Vetor Posição que localiza o referencial B em relação ao referencial A

Vetor Posição que localiza a partícula em relação ao referencial A

Vetor Posição que localiza a partícula em relação ao referencial B

Vetor Velocidade do referencial B em relação ao referencial A

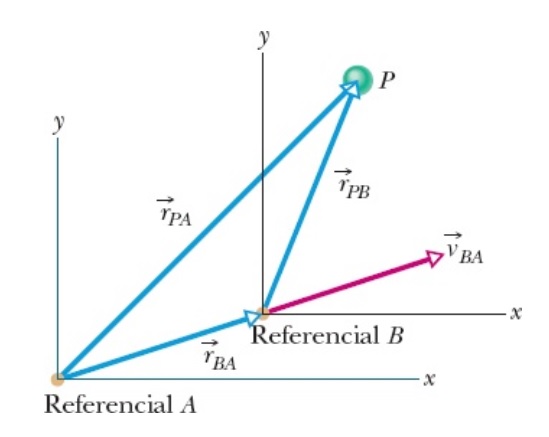
Utilizando a soma de vetores, temos que

\vec{r}_{PA}=\vec{r}_{BA}+\vec{r}_{PB}

Se derivarmos em relação ao tempo, obteremos

\frac{d\vec{r}_{PA}}{dt}=\frac{d\vec{r}_{BA}}{dt}+\frac{d\vec{r}_{PB}}{dt}

\vec{v}_{PA}=\vec{v}_{BA}+\vec{v}_{PB}

Se derivarmos novamente em relação ao tempo, obtemos

\frac{d\vec{v}_{PA}}{dt}=\frac{d\vec{v}_{BA}}{dt}+\frac{d\vec{v}_{PB}}{dt}

Como a derivada em relação ao tempo da velocidade do referencial B em relação ao tempo é nula, porque esta velocidade é constante, tem-se

\frac{d\vec{v}_{BA}}{dt}=0

logo,

\vec{a}_{PA}=\vec{a}_{PB}

Se a aceleração do referencial em movimento (Referencial B) for diferente de zero, ou seja, se a velocidade de B não for constante, tem-se

\vec{a}_{PA}=\vec{a}_{BA}+\vec{a}_{PB}

Este resultado é conhecido como o princípio da relatividade.

BIBLIOGRAFIA

HIBBELER, R. C. Dinâmica: Mecânica para Engenharia. Edição: 12 ed. São Paulo (SP): Pearson Universidades, 2010.

NUSSENZVEIG, H. M. Curso de Física Básica: Mecânica. Edição: 5 ed. [s.l.] Blucher, 2013.

RESNICK, R.; WALKER, J.; HALLIDAY, D. Fundamentos de Física – Volume 1 – Mecânica. Edição: 10 ed. [s.l.] LTC, 2016.

SERWAY, R.; JEWETT, J. Princípios de física – vol. I: Volume 1. Edição: 2 ed. [s.l.] Cengage Learning, 2014.

YOUNG, H. D.; FREEDMAN, R. A. Física de Sears & Zemansky: Volume I: Mecânica: Volume 1. Edição: 14 ed. [s.l.] Pearson Universidades, 2015.