Um carro, com 1300 kg de massa, em um parque de diversões se desloca sem atrito ao longo da pista indicada na figura 1.
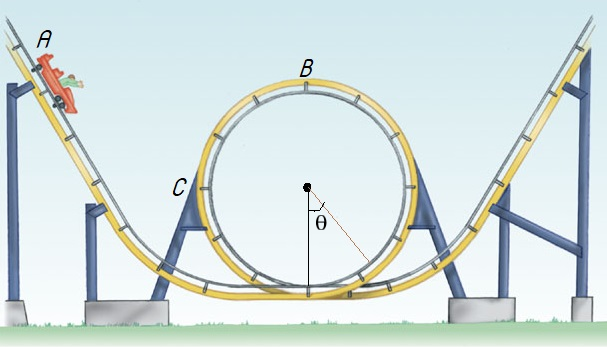
No diagrama esquemático da figura 2, o carro parte do repouso no ponto A situado a uma altura h acima da base do círculo com raio igual a R. Considera o carro como uma partícula.
Figura 1: Carro em looping; Fonte:https://onomeister.files.wordpress.com/2012/06/xgames-hot-wheels.jpg
Figura 2: Diagrama esquemático
I – Considere o caso em que e que , a velocidade da partícula se anula para qualquer valor de θ no intervalo informado, quando a força normal que a pista exerce sobre o carro é dada por:
N=mgcos \theta
e o ângulo em que ocorre isto for dado por:
\theta = \arccos \left( 1 – \frac{h}{R} \right)
II – Considere o caso em que e que , a força normal se anula, para qualquer valor de θ no intervalo informado, quando a velocidade do carro for dada por:
1 – O usuário deve ser informar o valor do raio de curvatura da pista, que deve pertencer ao intervalo ;
2 – O usuário deve ser informar o valor da altura acima da base do looping ao ponto A, que deve pertencer ao intervalo ;
3 – O programa deve informar a velocidade , a força normal exercida pela pista sobre o carro N, o ângulo em que ocorre um dos eventos listado no desenvolvimento do modelo θ, e as acelerações radial, tangencial e resultante se o carro chegar a executar o looping;
4 – O autor do projeto deve considerar as condições desenvolvidas acima.
