Cinemática de Rotação

O movimento de rotação tem um importante papel na Mecânica, isto porque podemos identificar uma grande quantidade de aplicações envolvendo rotação de uma partícula, de um conjunto de partículas ou até mesmo de corpos rígidos, tais como, um menino brincando de bole-bole, um porteiro abrindo uma porta, engrenagens de máquinas industriais, toda discos e players de CD e DVD, rodas de veículos e, o movimento dos corpos celestes, só para listar alguns dos exemplos.

ROTAÇÃO DE UMA PARTÍCULA

Iniciaremos a análise do movimento de rotação de uma partícula de massa m, movendo-se em uma trajetória circular com raio constante, definindo a grandeza posição angular da partícula, que é o ângulo formado entre o eixo x positivo com o vetor posição da partícula dado por

\vec{r}=x \hat{i} + y \hat{j}=rcos \theta \hat{i}+ rsen \theta \hat{j}

O movimento de rotação é caracterizado, entre outras coisas, pela mudança da posição angular θ, visto que não há alteração do raio da trajetória da partícula, tal alteração faz com que o vetor posição da partícula também seja alterado, conforme passa o tempo. É importante saber que um movimento circular, o mais simples possível, é acelerado e que o módulo do vetor posição da partícula é igual ao raio da trajetória $r = \left | \vec{r} \right |$ .

Resultando da mudança de posição angular da partícula, podemos definir a grandeza deslocamento angular, e dividindo-se pela variação do tempo do deslocamento, nos leva a definição de velocidade angular média, dada por

\omega_{m}=\frac{\Delta\theta}{\Delta t}=\frac{\theta_{f}-\theta_{i}}{t_{f}-t_{i}}

Estudaremos dois movimentos circulares importantes, o primeiro cuja velocidade angular ω é constante e o segundo cuja aceleração angular α é constante, o que equivale dizer, que a velocidade angular varia linearmente com o tempo, como veremos mais adiante.

MOVIMENTO CIRCULAR UNIFORME – MCU

O primeiro movimento é chamado de Movimento Circular Uniforme (MCU), e podemos encontrar a primeira equação utilizando-se o conceito de velocidade angular média, e adotando as seguintes características:

(i) Faremos t_i = 0 e t_f = t, onde t é um instante qualquer do movimento;

(ii) Tomaremos ω_m = ω com ω constante;

(iii) E a aceleração angular α nula;

Assim, podemos escrever a função horária da posição angular do MCU como sendo

\theta_{f}=\theta_{i}+wt

Analogamente, utilizando-se a velocidade instantânea, podemos definir a velocidade angular instantânea ω

\begin{matrix} \omega=\displaystyle\frac{d \theta}{dt} \\ \displaystyle\int_{\theta{i}}^{\theta_{f}}d\theta=\int_{0}^{t} \omega dt = \omega \int_{0}^{t} dt \\ \theta_{f}=\theta_{i}+\omega t \end{matrix}

Façamos a análise do comportamento do vetor velocidade da partícula, que não é uma grandeza constante, apesar de seu módulo permanecer constante no MCU. A figura nos mostra que a variação do vetor velocidade, forma um triângulo onde o ângulo Δθ oposto ao vetor é formado pelos vetores velocidade final e velocidade inicial e considerando-o muito pequeno, podemos fazer que o triângulo formado pelas velocidades pode ser aproximado ao arco da circunferência, dado por

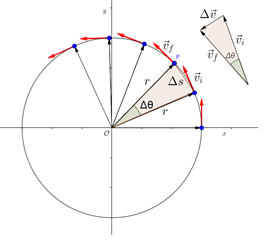
\begin{cases} \Delta s = r \Delta \theta \\ \Delta v = v \Delta \theta \end{cases}

Relação geométrica do arco de uma circunferência de raio r com o arco formado pelos vetores velocidades, quando é muito pequeno. Na figura o ângulo está exagerado.

se dividirmos ambas as equações pelo intervalo de tempo associado ao movimento, tem-se

\begin{cases} \displaystyle\frac{\Delta s}{\Delta t} = r \frac{\Delta \theta}{\Delta t} \\ \\ \displaystyle\frac{\Delta v}{\Delta t} = v \frac{\Delta \theta}{\Delta t} \end{cases}

e, portanto

\begin{cases} v = r \omega\\ a_{c} =v\omega \end{cases}

o que, por fim, combinando-se as equações acima, nos leva a definição de aceleração centrípeta

a_{c}=\frac{v^{2}}{r}

Tomemos agora, o caso em que a velocidade de translação da partícula muda com o tempo, isso ocorre por causa do surgimento de uma aceleração na direção tangencial ao raio, que chamaremos de aceleração tangencial a_t.

Inicialmente, consideraremos que a aceleração tangencial é constante, o que nos permite dizer que, como a velocidade de translação da partícula em movimento circular vai variar, a velocidade angular da partícula também irá variar, logo, para os instantes arbitrários t₁ e t₂, teremos as velocidades angulares associadas ω₁ e ω₂, desta forma podemos definir a aceleração angular α como sendo a grandeza que mede como a velocidade angular da partícula varia, assim

\alpha_{m}=\frac{\Delta \omega}{\Delta t}=\frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}

A equação acima define a aceleração angular média α_m, esta definição carrega a mesma limitação que observamos nas outras grandezas definidas desta forma, se no intervalo de tempo Δt a velocidade angular da partícula variar, mas voltar a ter o mesmo valor que possuía inicialmente, então a aceleração angular será nula. Definiremos a grandeza aceleração angular instantânea α como sendo,

\alpha=\lim_{\Delta t\rightarrow 0}\frac{\Delta \omega}{\Delta t}=\frac{d\omega}{dt}

MOVIMENTO CIRCULAR UNIFORMEMENTE VARIADO – MCUV

Podemos adotar as características que definirão o chamado Movimento Circular Uniformemente Variado (MCUV), como se segue

(i) Faremos t_i = 0 e t_f = t, onde t é um instante qualquer do movimento;

(ii) Tomando-se α_m = α e fazendo α contante;

obtem-se

\alpha = \frac{\omega_{2}- \omega_{1}}{t-0} \implies \omega_{2}=\omega_{1}+\alpha t

a equação acima é conhecida como função horária da velocidade angular para o MCUV. Podemos escrever que

\omega = \frac{d\theta}{dt}=\omega_{i}+\alpha t \implies \int_{\theta_{i}}^{\theta_{f}}d \theta=\int_{0}^{t}(\omega_{i}+\alpha t)dt

logo,

\theta_{f}=\theta_{i}+\omega_{i}t+\frac{1}{2}\alpha t^{2}

a equação acima é conhecida como função horária da velocidade angular para o MCUV.

Uma importante equação do MCUV relaciona as velocidades angulares com o deslocamento angular e a aceleração angular, esta equação é semelhante à equação de Torricelli,

\omega_{f}^{2}=\omega_{i}^{2}+2\alpha \Delta\theta

A aceleração tangencial é determinada a partir da equação que relaciona a velocidade tangencial com a velocidade angular, derivando-a em função do tempo, o que nos dá

\frac{dv}{dt}=r\frac{d\omega}{dt} \implies a_{t}=r\alpha

O vetor aceleração para o MCUV é definido como sendo,

\vec{a}=a_{t}\hat{\theta}-a_{c}\hat{r}

Onde os vetores unitários radial e tangential são, respectivamente

\begin{cases} \hat{r}=cos \theta \hat{i}+ sen \theta \hat{j} \\ \hat{\theta}= -sen \theta \hat{i} + cos \theta \hat{j} \end{cases}