Dinâmica de Rotação

TORQUE

Iniciaremos o estudo do torque considerando um corpo rígido qualquer como o mostrado na figura, que está rotacionando em torno de um eixo que passa por O e seu centro de massa executa uma trajetória circular de raio R, devido a uma força F aplicada no ponto P cujo vetor r determina sua posição. Sabemos que uma força aplicada sobre um corpo que se desloca no espaço faz com que este corpo mude seu estado, neste caso, entenderemos que nos referimos às grandezas físicas que caracterizam o movimento, posição, velocidade e aceleração, cabe investigar o que pode alterar ou causar um movimento de rotação, tal é o interesse de estudarmos a grandeza torque.

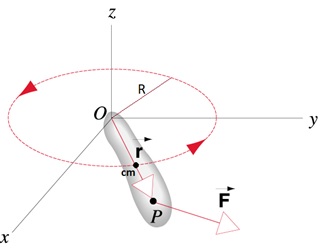
Simplificando nossa análise, consideraremos uma partícula de massa m se movimentando em uma trajetória circular de raio r sobre a ação de uma força aplicada F, que possui componentes radial e tangencial,  e , respectivamente.

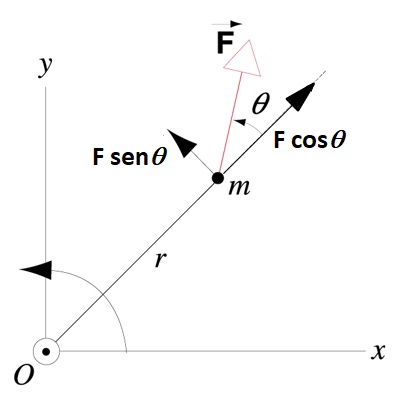
Levando em consideração que o ponto O não se moverá, a única componente da força que contribui para o movimento de rotação é a componente tangencial . Podemos afirmar que a componente perpendicular da força é a responsável pela rotação da massa m, em torno do eixo que passa por O, no entanto, devemos considerar outro fator para entendermos o conceito de torque, que é o valor de r. Quando um marceneiro instala uma maçaneta em uma porta, ele fixa a mesma num ponto afastado do eixo de rotação da porta, isso porque, quando abrirmos a porta, aplicaremos uma força menor do que seria aplicado se a maçaneta fosse instalada próxima ao eixo de rotação, o mesmo fato se observa quando queremos desparafusar as rodas de um carro quando este tem um pneu furado, note que para executarmos uma força menor aplicamos a força no ponto mais afastado do eixo de rotação do parafuso, portanto, vemos claramente que há uma dependência direta do torque com a distância de aplicação da força a partir do eixo de rotação, que no nosso caso é representado pela grandeza r, assim podemos definir o módulo do torque como sendo o produto da componente tangencial da força aplicada pela distância do eixo de rotação ao ponto de aplicação da força;

\tau = rF_{t} = r F sen \theta

COMPORTAMENTO VETORIAL DO TORQUE

Estudaremos o produto vetorial de forma a considerarmos o caso mais geral, levando-se em conta que todos os vetores são escritos como combinação linear dos vetores de base canônicos , logo, temos que e .

Por definição, temos que o módulo do produto vetorial é determinado pelo produto dos módulos dos vetores envolvidos no produto, com o produto do seno do ângulo formado pelos mesmos vetores, ou seja,

\left |\vec C  \right | = \left |\vec A \times \vec B  \right | = ABsen \theta

De modo geral, o produto vetorial é determinado por

\begin{aligned}
\vec A \times \vec B & =  A_{x} \hat i \times B_{x} \hat i + A_{x} \hat i \times B_{y} \hat j + A_{x} \hat i \times B_{z} \hat k + \\
 & + A_{y} \hat j \times B_{x} \hat i + A_{y} \hat j \times B_{y} \hat j + A_{y} \hat j \times B_{z} \hat k + \\
 & + A_{z} \hat k \times B_{x} \hat i + A_{z} \hat k \times B_{y} \hat j + A_{z} \hat k \times B_{z} \hat k
\end{aligned}

Sabemos que o resultado do produto vetorial entre dois vetores tem como resultado um terceiro vetor perpendicular ao plano formado pelos vetores do produto, e que pela definição de produto vetorial, se um vetor é multiplicado por ele mesmo o resultado é nulo, pois o ângulo formado é zero, dessa forma temos como resultado o seguinte,

\begin{cases}
\hat i \times \hat i = \hat j \times \hat j = \hat k \times \hat k = 0 \\
\hat i \times \hat j = \hat k \text{ e }\hat j \times \hat i = - \hat k \\
\hat j \times \hat k = \hat i \text{ e }\hat k \times \hat j = - \hat i \\
\hat k \times \hat i = \hat j \text{ e }\hat i \times \hat k = - \hat j 
\end{cases}

Com estes resultados, podemos reduzir a equação acima na forma

\begin{aligned}
   \vec A \times \vec B  & =A_{x}B_{y} \hat k - A_{x}B_{z} \hat j - A_{y}B_{x} \hat k + A_{y}B_{z} \hat i + A_{z}B_{x} \hat j - A_{z}B_{y} \hat i  \\
      & = (A_{y}B_{z} - A_{z}B_{y})\hat i + (A_{z}B_{x} -A_{x}B_{z}) \hat j + (A_{x}B_{y} - A_{y}B_{x}) \hat k
\end{aligned}

Este resultado também pode ser encontrado calculando-se o determinante da seguinte matriz,

\vec A \times \vec B = \begin{vmatrix}
\hat i & \hat j & \hat k \\
A_{x} & A_{y} & A_{z} \\
B_{x} & B_{y} & B_{z}
\end {vmatrix}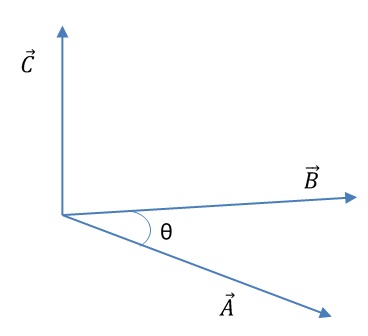

Podemos associar um vetor unitário às grandezas de rotação, isso porque, como podemos verificar, o torque indica o sentido de rotação de uma partícula, quando esta está sobre a ação de uma força aplicada, tal força determinará o sentido do torque.

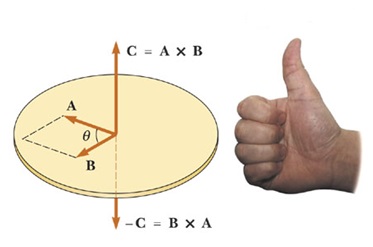
A definição de produto vetorial indica que o torque deve estar associado ao vetor C da figura acima, permitindo que sejamos capazes de enunciar algumas regras que indiquem a direção e o sentido do torque. Essa regra é conhecida como a regra da mão direita, o vetor A é representado pelo polegar, o vetor B pelo dedo indicador e o vetor C pelo dedo médio, podemos ainda determinar o sentido de rotação considerando o sentido de fechamento da mão direita, como identificado na imagem, este sentido pode ser associado à velocidade angular ω, dizendo se o sentido de rotação é anti-horário ou horário.

Devemos perceber que mudando a ordem do produto mudamos o sentido do vetor C, de forma geral o torque vetorial produzido por uma força F aplicada no ponto determinado pelo vetor r, pode ser definido como

\vec \tau = \vec r \times \vec F

Estabeleceremos que quando o movimento for anti-horário teremos um movimento progressivo, de modo a obedecer a forma com a qual o círculo trigonométrico varia, e o movimento será retrógrado quando o sentido de rotação for horário. Devemos tomar cuidado com o sentido da aceleração angular, pois quando esta tiver o mesmo sentido da velocidade angular o movimento será acelerado e se o sentido for oposto, o movimento será desacelerado.

REGRA DA MÃO DIREITA

Tratemos o caso em que N forças estão sendo aplicadas em uma partícula de massa m e que executa um movimento circular de raio r, desta forma cada força realizará um torque sobre a partícula, de modo que

\vec \tau_{1} + \vec \tau_{2} + \vec \tau_{3}+ \dots + \vec \tau_{N} = \vec \tau_{R}

onde é o torque resultante aplicado ao corpo de massa m, dessa forma podemos escrever,

\vec \tau_{R} = \vec r \times \vec F_{1} + \vec r \times \vec F_{2} + \dots +\vec r \times \vec F_{N} 

com módulo,

\left |\vec \tau_{R}  \right| = r \sum_{i=1}^{N}F_{ti} = rma_{t}=mr^2\alpha = I \alpha

tendo-se F_ti como sendo a somatória de todas as componentes tangenciais das forças que atuam no corpo de massa m, e I é o momento de inércia da partícula de massa m, de modo geral, podemos definir a segunda lei de Newton para a rotação como sendo,

\vec \tau_{R} = I \alpha

a equação acima afirma que o torque resultante é igual ao produto do momento de inércia da partícula de massa m pela sua aceleração angular, aqui devemos perceber que o torque resultante tem a mesma direção e o mesmo sentido da aceleração angular.

ENERGIA CINÉTICA DE ROTAÇÃO

Continuemos analisando o caso de uma partícula movendo-se em uma trajetória circular de raio r, e determinemos o valor da energia cinética desta partícula de massa m, sabemos que a energia cinética é definida por

E_{CR} = \frac{1}{2}mv^2=\frac{1}{2}m(r \omega)^2=\frac{1}{2}(mr^2)\omega^2=\frac{1}{2}I\omega^2

logo, a energia cinética de rotação é dada pela expressão acima, que como veremos, é geral, valendo para corpos rígidos também.

Consideremos que um corpo rígido é formado por várias pequenas porções de massas m_i e que cada uma destas porções tem uma velocidade v_i, e que cada massa é localizada por um vetor r_i, mas que gira em torno de um determinado eixo com velocidade angular ω, a energia cinética de rotação total deste corpo rígido será

E_{CR}=\sum_{i=1}^{N}\frac{1}{2}m_{i}v_{i}^{2}=\frac{1}{2}I\omega^2

onde  é o momento de inércia de cada partícula que compõe o corpo rígido, portanto, como queremos somar todos os pequenos pedaços que formam o corpo rígido teremos

I = \lim_{m_i \rightarrow 0} \sum_{i=1}^{N}m_ir_i^2 = \int r^2 dm