OSCILAÇÕES SIMPLES
Uma função f:ℝ→ℝ é dita periódica de período T (também chamada de T-periódica) se existe uma constante positiva T tal que
f(t) = f(t+T)
para todo t ∈ ℝ.
Algumas funções periódicas admitem um menor período, chamado de período fundamental. A frequência fundamental é então dada por f=1/T e a frequência angular fundamental é dada por wf = 2πf.
Oscilador Massa-Mola
Utilizando-se a segunda Lei de Newton e analisando as força que atuam no corpo de massa m, podemos verificar que há sobre a massa uma força peso P, uma força elástica Fel, a força normal N e sem força de atrito entre o bloco e a superfície.
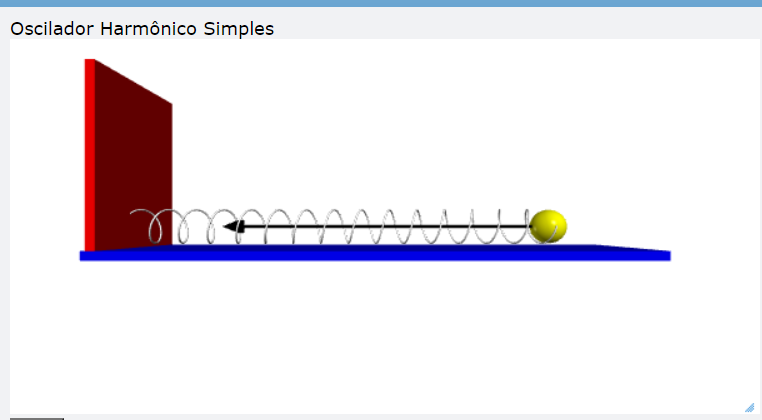
logo, aplicando a Segunda Lei de Newton
\vec{F}_{R} = m \vec{a} \\
\vec{F}_{el} + \vec{P} + \vec{N} = m \vec{a} \\como a força peso P é igual a força normal N
\vec{F}_{el} = m \vec{a}considerando o movimento em uma dimensão 1D, tem-se
-kx = m \frac{d^2x}{dt^2} \\
\frac{d^2x}{dt^2} + \frac{k}{m} x = 0a equação acima é chamada de equação de movimento do oscilador harmônico simples OHS, defini-se a frequência angulardo oscilador massa-mola por
\omega^2=\frac{k}{m}portanto, pode-se escrever que
\frac{d^2x}{dt^2} + \omega^2 x = 0Uma possível solução para a equação de movimento do OHS é a função
x(t) = A \cos (\omega t + \theta_{0})Faça a prova!
Pode-se determinar a velocidade e a aceleração do OHS, logo
v_{x} = \frac{dx}{dt} = -A \omega \sin(\omega t + \theta_{0}) \\
v_{x,max} = A \omegaa_{x} = \frac{dv_{x}}{dt} = -A\omega^2 \cos(\omega t + \theta_{0})\\
a_{x,max} = A \omega^2Obtendo relações entre as grandezas
\sin^2 \theta +\cos^2 \theta = 1 \\
\left(-\frac{v_{x}}{A \omega}\right)^2 + \left(\frac{x}{A}\right)^2 = 1 \\
\left(\frac{v_{x}}{ \omega}\right)^2 + x^2 = A^2e
\sin^2 \theta +\cos^2 \theta = 1 \\
\left(-\frac{v_{x}}{A \omega}\right)^2 + \left(-\frac{a_{x}}{A\omega^2}\right)^2 = 1 \\
v_{x}^{2} + \left(\frac{a_{x}}{\omega}\right)^2 = A^2 \omega^2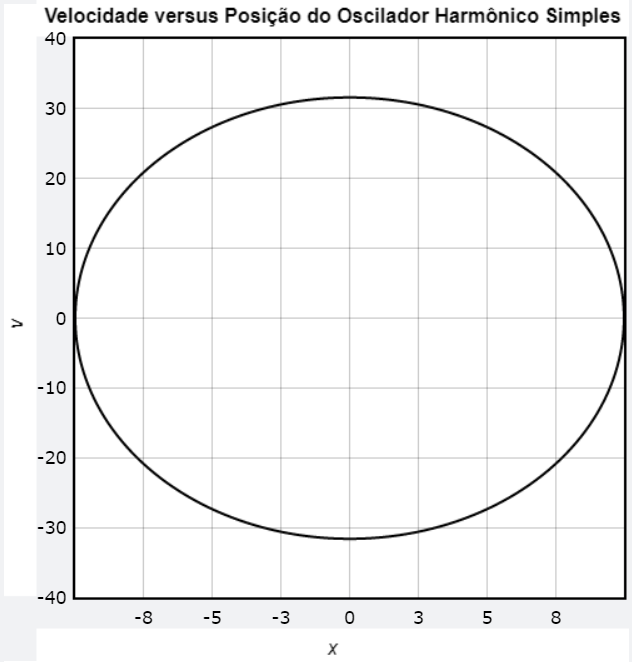
Energia no OHS
A energia cinética de um corpo em movimento é determinada pela expressão
E_{C} = \frac{1}{2}mv^2Como vimos acima, a velocidade de um oscilador harmônico varia com o tempo e é descreita por uma função periódica, logo
E_{C} = \frac{1}{2} m \left[-A \omega \sin (\omega t + \theta_{0}) \right]^2 \\ ou \\
E_{C} = \frac{1}{2} m A^2 \omega^2 \sin^2 (\omega t + \theta_{0})A energia potencial no sistema massa-mola é elástica, portanto
U = \frac{1}{2} k x^2 Como sabemos, a posição de um oscilador harmônico varia com o tempo e é uma função periódica, assim
U = \frac{1}{2} k \left[ A \cos (\omega t + \theta_{0}) \right]^2 \\
ou
\\
U = \frac{1}{2} k A^2 \cos^2 (\omega t + \theta_{0})A energia mcânica ao contrário do que se espera não varia com o tempo, mantendo-se constante, dada por
E = E_{C} + UE = \frac{1}{2} m A^2 \omega^2 \sin^2 (\omega t + \theta_{0}) + \frac{1}{2} k A^2 \cos^2 (\omega t + \theta_{0})Se utilizarmos a expressão,
\omega^2 m=k
logo,
E = \frac{1}{2} A^2k \sin^2(\omega t + \theta_{0}) + \frac{1}{2} A^2 k \cos^2(\omega t + \theta_{0}) Utilizando-se
\sin^2 \theta + \cos^2 \theta = 1
temos,
E = \frac{1}{2} kA^2 = \frac{1}{2}mA^2 \omega^2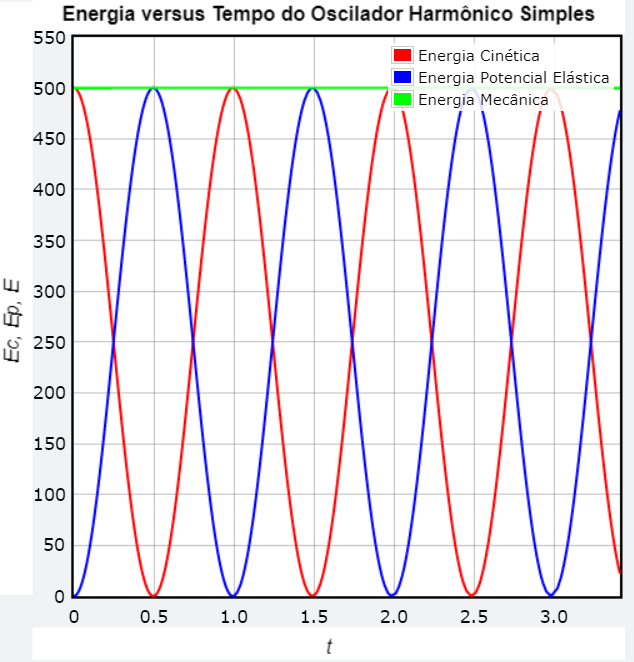
OSCILAÇÕES AMORTECIDAS
Chamamos de amortecimento a diminuição da amplitude provocada por uma força dissipativa e de oscilação amortecida o movimento correspondente.
Se considerarmos o sistema massa-mola submetido a uma força dissipativa proporcional à velocidade, do tipo
\vec{F}_{d} = -b\vec{v} A equação de movimento para este oscilador dependerá da força elástica e da força dissipativa
\vec{F}_{R} = \vec{F}_{el} + \vec{P} + \vec{N} + \vec{F}_{d} = m\vec{a}como a força peso se anula com a força normal, tomando-se o sistema oscilando ao longo do eixo x, em movimento 1D, tem-se
-kx-bv_{x}=m\frac{d^2x}{dt^2}Reescrevendo a equação acima,
\frac{d^2x}{dt^2} + \frac{b}{m}\frac{dx}{dt} + \frac{k}{m}x = 0Uma boa prática é definirmos o operador matemático
D = \frac{d}{dt} \\
\text{e} \\
D^2 = \frac{d^2}{dt^2}pode-se escrever a equação de movimento na forma
D^2x + \frac{b}{m}Dx + \frac{k}{m}x = 0 \\
\text{logo,} \\
\left(D^2 + \frac{b}{m}D + \frac{k}{m}\right)x = 0Resolvendo a equação do segundo grau dentro dos parenteses, temos
D = - \frac{b}{2m} \pm \sqrt{\left( \frac{b}{2m}\right)^2-\frac{k}{m}}O termo da frequência pura do oscilador ω0, sem a influência do amortecimento é predominante, e dado por
\omega_{0}^2 = \frac{k}{m} Ajustando a equação de D, teremos
D = -\frac{b}{2m} \pm \sqrt{-1}\sqrt{\omega_{0}^2 - \left(\frac{b}{2m}\right)^2}com
i = \sqrt{-1}A equação acima apresenta dois valores para D, o que nos sugere que uma possível solução é uma combinação linear de exponenciais complexas de t, assim,
x(t) = C_{1}\exp(D_{1}t) + C_{2}\exp(D_{2}t)teremos,
x(t) = C_{1}\exp{\left[t \left( -\frac{b}{2m}+i\sqrt{\omega_{0}^2-\left( \frac{b}{2m} \right)^2} \right) \right]} + \\ +C_{2}\exp{\left[t \left( -\frac{b}{2m}-i\sqrt{\omega_{0}^2-\left( \frac{b}{2m} \right)^2} \right) \right]}Utilizando-se a condição de que,
C_{1} = C_{2} = \frac{A}{2}podemos reescrever a equação acima como,
x(t) = \frac{A}{2} \exp{\left( -\frac{b}{2m}t\right)} \exp{\left[t \left( +i\sqrt{\omega_{0}^2-\left( \frac{b}{2m} \right)^2} \right) \right]} + \\ +\frac{A}{2} \exp{\left( \frac{b}{2m}t\right)} \exp{\left[t \left( -i\sqrt{\omega_{0}^2-\left( \frac{b}{2m} \right)^2} \right) \right]}simplificando,
x(t) = \frac{A}{2} \exp{\left( -\frac{b}{2m}t \right)} \left\{ \exp{(+it\omega')} + \exp{(-it\omega')} \right\}onde ω’ é a frequência angular do oscilador amortecido, dada por
\omega' = \sqrt{\omega_{0}^2 - \left(\frac{b}{2m}\right)^2}Utilizando a identidade
\cos{z} = \frac{e^{iz}+e^{-iz}}{2}Logo, acrescentando a influência da constante de fase θ0
x(t) = \displaystyle{A e^{-\frac{b}{2m}t}\cos{(\omega' t + \theta_{0})}}A equação acima é a uma solução da equação de movimento do Oscilador Amortecido, deixaremos que o estudante tire a prova.
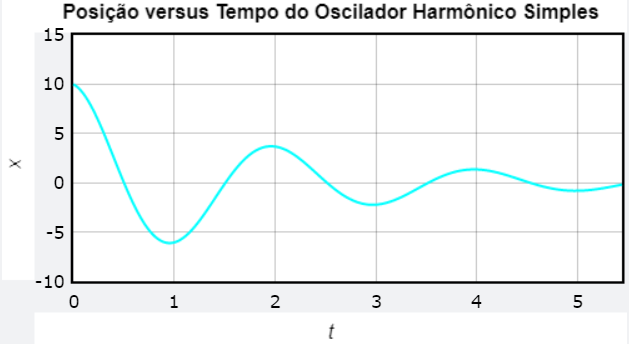
Podemos realizar o estudo da frequência do oscilador amortecido, vemos que quando o valor de b é menor que o valor crítico, que é
\text{se }\omega' \rightarrow 0 \text{, temos que, } \frac{k}{m} - \frac{b^2}{4m^2} = 0e o valor crítico de b é dado por
b = 2\sqrt{km}Na condição acima de b, tem-se um amortecimento crítico.
Para b menor que o valor crítico, a condição denomina-se subamortecimento.
A condição onde b é maior que o valor crítico corresponde ao superamortecimento.
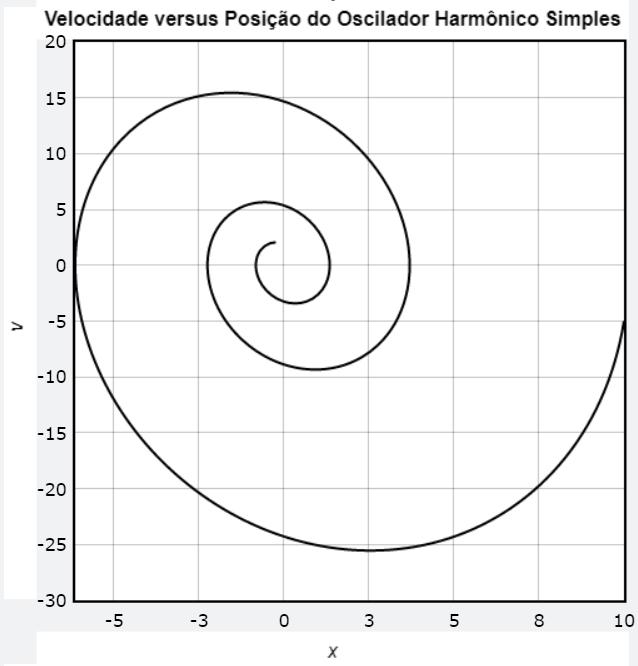
Nas oscilações amortecidas, a força do amortecimento não é conservativa; a energia mecânica do sistema não é constante e diminui continuamente, tendendo a zero depois de um longo tempo.
A taxa de variação da energia pode ser calculada utilizando-se
\frac{dE}{dt} = \frac{dE_{C}}{dt} + \frac{dU_{el}}{dt}as derivadas são
\frac{dE}{dt} = \frac{1}{2}m \left(2v \frac{dv}{dt}\right) + \frac{1}{2}k \left(2x\frac{dx}{dt} \right)simplificando
\frac{dE}{dt} = v \left( m \frac{dv}{dt} + kx\right)o termo dentro dos parenteses é obtido pela equação de movimento, logo
m \frac{dv}{dt} + kx = -bvassim,
\frac{dE}{dt} = -bv^2A equação acima informa que, a taxa de variação da energia mecânica total é igual ao negativo da taxa com a qual a força do amortecimento realiza trabalho sobre o sistema.

PÊNDULO SIMPLES
O pêndulo smples é um modelo físico ideal, leva em consideração o comportamento de uma partícula de massa m presa em um fio de comprimento L com massa desprezível e inextensível, com a outra extremidade do fio presa em um ponto fixo.
A partícula é levemente puxada para a lateral, produzindo um deslocamento angular θ, removendo-a de seu estado de equilíbrio. Neste ponto, a força peso atua como uma força restauradora, fanzendo a partícula retornar ao seu ponto de equilíbrio, desprezando-se a força de arrasto do ar, a energia inicial imprimida ao pêndulo é conservada fazendo com que a partícula execute um movimento periódico, ver figura.
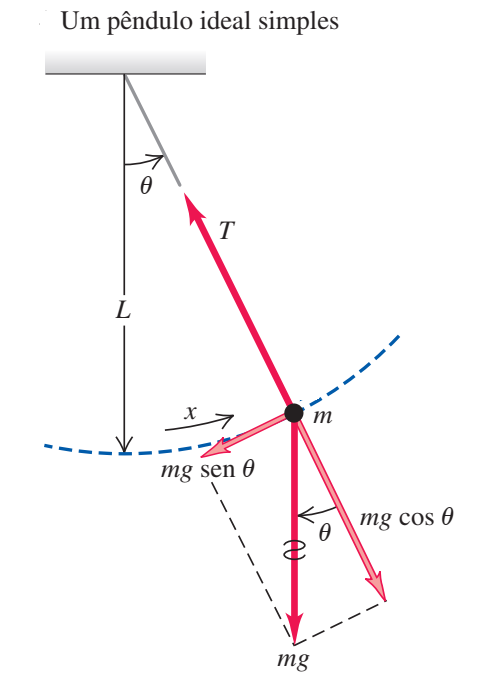
Como vemos na figura, a partícula executa ummovimento circular de raio L, desta maneira podemos escrever que o valor de x é dado por
x = \theta L
A componente tangencial do peso é a força restauradora, portanto
F_{t}=-mg\sin{\theta}Destaca-se ainda, a força tangencial como sendo o produto da massa da partícula por sua aceleração tangencial at dada por
\displaystyle{F_{t}=ma_{t}}\\
.
\\
\displaystyle{a_{t}=\frac{d^2x}{dt^2} }\\
. \\
\displaystyle{a_{t}=L \frac{d^2 \theta}{dt^2}}A equação de movimento do pêndulo simples é dada por
mL \frac{d^2\theta}{dt^2}+mg\sin{\theta}=0 \\
. \\
\frac{d^2 \theta}{dt^2}+\left(\frac{g}{L}\right)\sin{\theta}=0A equação de movimento acima é não-linear e não se caracteriza como um oscilador harmônico simples, no entanto, se utilizarmos o resultado para pequenos ângulos sen(θ) ≈ θ , a equação passa ter as mesmas características do oscilador simples
\frac{d^2 \theta}{dt^2}+\left(\frac{g}{L}\right)\theta=0Temos, como resultado para a frequência angular ω, quando θ for muito pequeno, a expressão
\omega^2 = \frac{g}{L}Logo, o período será
T = 2 \pi \sqrt{\frac{L}{g}}Note que o período das pequenas oscilações não dependa da massa m da partícula.
OSCILAÇÕES FORÇADAS
Oscilação forçada é o movimento de um sistema que oscila sob a influência contínua de uma força externa oscilante , diferente de uma oscilação livre (sem força externa) ou amortecida (com atrito). A chave é que uma força externa, como um empurrão periódico em um balanço ou uma vibração, impõe sua própria frequência ao sistema, que passa a oscilar com a frequência dessa força (regime estacionário), e não com sua própria frequência natural, podendo levar à ressonância quando as frequências coincidem, resultando em amplitudes muito grandes.
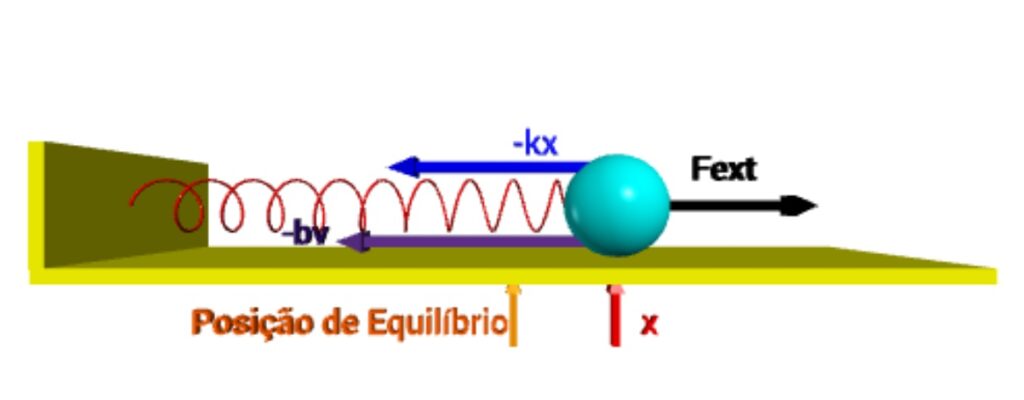
A força resultante ao longo da direção x será
m a_{x}=-bv_{x}-kx+F_{ext}a força externa oscilante tem a forma
F_{ext} = F_{0}cos \omega_{f} ta equação de movimento ficará
\frac{d^2x}{dt^2}+\frac{b}{m}\frac{dx}{dt}+\frac{k}{m}x=\frac{F_{0}}{m}\cos \omega_{f} tlogo, com e
\frac{d^2x}{dt^2}+2\gamma\frac{dx}{dt}+\omega_{0}^2 x=\frac{F_{0}}{m}\cos \omega_{f} tA solução geral é determinada pela combinação linear da solução estacionária , dada por
x_{1}(t)=A\cos \omega_{f} t + B \sin \omega_{f} te a solução transiente
x_{2}(t)=e^{-\gamma t}(C\cos \omega t+D\sin \omega t)onde,
portanto,
x(t)=A\cos \omega_{f} t + B \sin \omega_{f} t + e^{-\gamma t}(C\cos \omega t+D\sin \omega t)A velocidade do oscilador forçado é
v(x)=\frac{dx}{dt}=-A\omega_{f}\sin \omega_{f} t + B \omega_{f} \cos\omega_{f} t- \\
- \gamma e^{-\gamma t}(C\cos \omega t + D \sin\omega t)+\omega e^{-\gamma t}(C cos \omega t + D \sin \omega t)Começemos analisando a solução estacionária na seguinte forma
x(t)=A_{0}\sin ({\omega_{f} t- \delta})podemos reescrever a equação como
x(t)=A_{0}\sin \omega_{f}t \cos \delta-A_{0}\cos\omega_{f}t\sin\deltaCalculando-se a primeira e segunda derivadas, tem-se
\frac{dx}{dt}=A_{0}\omega_{f}\cos\delta\cos\omega_{f}t+A_{0}\omega_{f}\sin\delta\sin\omega_{f}ttambém,
\frac{d^2x}{dt^2}=-A_{0}\omega_{f}^2\cos\delta\sin\omega_{f}t+A_{0}\omega_{f}^2\sin\delta\cos\omega_{f}tSubstituindo na equação de movimento, teremos
-A_{0}\omega_{f}^2\cos\delta\sin\omega_{f}t+A_{0}\omega_{f}^2\sin\delta\cos\omega_{f}t+\\ +2\gamma(A_{0}\omega_{f}\cos\delta\cos\omega_{f}t+A_{0}\omega_{f}\sin\delta\sin\omega_{f}t)+\\
+\omega_{0}^2(A_{0}\sin \omega_{f}t \cos \delta-A_{0}\cos\omega_{f}t\sin\delta)=\frac{F_{0}}{m}\cos\omega_{f}t+0\sin\omega_{f}tOrganizando a equação acima e utilizando a indentidade na igualdade,
\left( A_{0}\omega_{f}^2\sin\delta+2\gamma A_{0}\omega_{f}\cos \delta-A_{0}\omega_{0}^2\sin \delta \right)\cos\omega_{f}t+\\
+\left( -A_{0}\omega_{f}^2\cos\delta+2\gamma A_{0}\omega_{f}\sin \delta+A_{0}\omega_{0}^2\cos \delta \right)\sin\omega_{f}t= \frac{F_{0}}{m}\cos\omega_{f}t+0\sin\omega_{f}tlogo, pela identidade
\begin{cases}
2\gamma \omega_{f} A_{0}\cos \delta-(\omega_{0}^2-\omega_{f}^2)A_{0}\sin\delta=\frac{F_{0}}{m} \\
(\omega_{0}^2-\omega_{f}^2)A_{0}\cos\delta+2\gamma \omega_{f} A_{0} \sin \delta=0
\end{cases}Resolvendo o sistema acima por substituição
2\gamma \omega_{f} A_{0}\cos \delta+\frac{(\omega_{0}^2-\omega_{f}^2)^2}{2\gamma\omega_{f}}A_{0}\cos\delta=\frac{F_{0}}{m} \\
. \\
A_{0}\cos \delta=\frac{2 \gamma \omega_{f}F_{0}}{m \left( (\omega_{0}^2-\omega_{f}^2)^2+4\gamma^2\omega_{f}^2 \right)}e
A_{0}\sin\delta=-\frac{(\omega_{0}^2-\omega_{f}^2)}{2\gamma\omega_{f}}A_{0}\cos\delta \\
.\\
A_{0}\sin\delta=-\frac{(\omega_{0}^2-\omega_{f}^2)F_{0}}{m \left( (\omega_{0}^2-\omega_{f}^2)^2+4\gamma^2\omega_{f}^2 \right)}utilizando-se,
A_{0}^2\cos^2\delta+A_{0}^2\sin^2\delta=\frac{(\omega_{0}^2-\omega_{f}^2)^2-4\gamma^2\omega_{f}^2}{ \left( (\omega_{0}^2-\omega_{f}^2)^2+4\gamma^2\omega_{f}^2 \right)^2}\frac{F_{0}^2}{m^2} \\
.\\
A_{0}=\frac{F_{0}/m}{\sqrt{\left( (\omega_{0}^2-\omega_{f}^2)^2+4\gamma^2\omega_{f}^2 \right)}}O resultado acima é a amplitude do oscilador forçado com amortecimento.
podemos calcular a relação da constante de fase
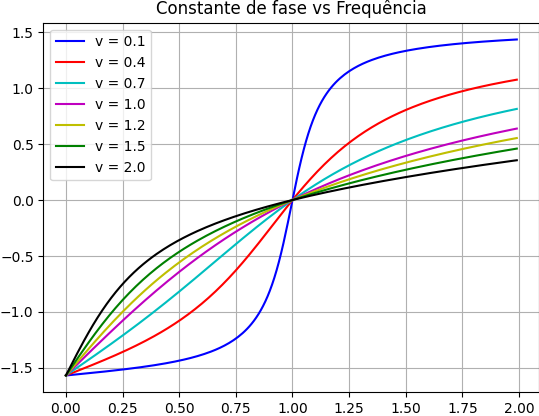
\tan\delta = \frac{\sin\delta}{\cos\delta}=\frac{\omega_{f}^2-\omega_{0}^2}{2\gamma \omega_{f}}Para analisarmos o comportamento nos gráficos da amplitude e da constante de fase em função da frequência, fazemos e
\begin{cases}
A_{0}m\omega_{0}/F_{0}= \displaystyle \frac{1}{\sqrt{(1-\tau^2)^2+4\nu^2\tau^2}} \\
\delta = \arctan\displaystyle\frac{\tau^2-1}{2\nu\tau}
\end{cases}Comportamento da Amplitude versus a frequência
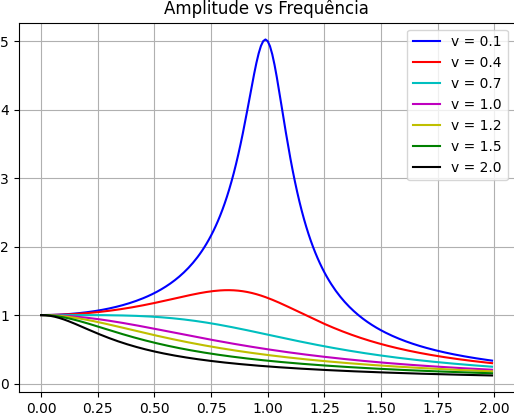
Nota-se que um pico acentuado vai se formando quando o amortecimento vai tendendo a zero e a frequência da força externa se iguala a frequência natural do oscilador .
Comportamento da constante de fase versus a frequência
ENERGIA DO OSCILADOR FORÇADO
Quando a força externa atua sobre o oscilador, ela realiza trabalho sobre ele e, portanto, cede energia para ele. A potência instantânea exercida pela força é
P(t)=F_{ext}(t)\frac{dx}{dt}Logo,
P(t)=F_{0}\cos(\omega_{f}t)A_{0}\omega_{f}\cos(\omega_{f}t-\delta)A potência varia durante o ciclo. O seu valor médio por ciclo é determinado com a média temporal de em um ciclo. Com , temos
P=\frac{1}{T}\int_{0}^{2\pi/\omega_{f}}{P(t)}dt \\
.\\
P=\frac{\omega_{f}}{2\pi}F_{0}A_{0}\omega_{f}\int_{0}^{2\pi/\omega_{f}}{\cos(\omega_{f}t)\cos(\omega_{f}t-\delta)dt} utilizemos a relação abaixo
\cos(\omega_{f}t)\cos(\omega_{f}t-\delta)=\cos(\omega_{f}t)(\cos(\omega_{f}t)\cos(\delta)+\sin(\omega_{f}t)\sin(\delta)) = \\
=\cos^2(\omega_{f}t)\cos(\delta)+\cos(\omega_{f}t)\sin(\omega_{f}t)\sin(\delta)= \\
=\cos^2(\omega_{f}t)\cos(\delta)+\frac{1}{2}\sin(2\omega_{f}t)\sin(\delta)tem-se que
P=\frac{\omega_{f}}{2\pi}F_{0}A_{0}\omega_{f}\left[\int_{0}^{2\pi/\omega_{f}} \cos^2(\omega_{f}t)\cos(\delta)dt+\int_{0}^{2\pi/\omega_{f}}\frac{1}{2}\sin(2\omega_{f}t)\sin(\delta)dt \right]a segunda integral vai zerar, ficando
P=\frac{\omega_{f}^2}{2\pi}F_{0}A_{0}\cos(\delta)\int_{0}^{2\pi/\omega_{f}} \cos^2(\omega_{f}t)dtassim,
P=\frac{\omega_{f}^2}{2\pi}F_{0}A_{0}\cos(\delta)\frac{\pi}{\omega_{f}} \\
.\\
P=\frac{\omega_{f}F_{0}}{2}\frac{2 \gamma \omega_{f}F_{0}}{m \left( (\omega_{0}^2-\omega_{f}^2)^2+4\gamma^2\omega_{f}^2 \right)} \\
.\\
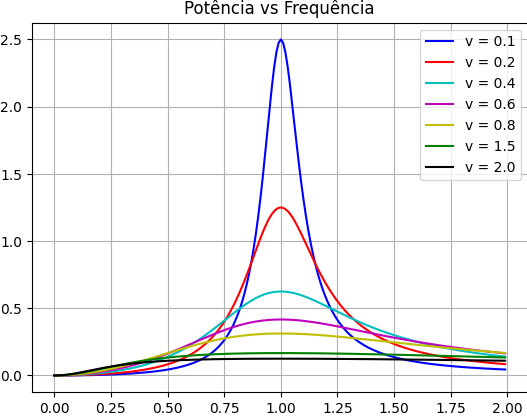
P=\frac{\gamma F_{0}^2\omega_{f}^2/m}{(\omega_{0}^2-\omega_{f}^2)^2+4\gamma^2\omega_{f}^2}fazemos e
P\omega_{0}m/F_{0}=\frac{\nu \ \tau^2}{(\tau^2-1)^2+4\nu^2\tau^2}Definindo a grandeza chamada de fator de qualidade Q, como . Note que o pico é maior e mais estreito para Q maiores.
OSCILAÇÃO FÍSICA
O pêndulo físico é um sistema físico descrito por um corpo que ocupa um espaço, um corpo rígido cuja força resultante sobre ele é restauradora, ocasionando um movimento periódico, que em pequenas oscilações descreve um MHS, caracterizado pela equação de movimento abaixo
\frac{d^2x}{dt^2}+\omega^2x=0A figura a seguir representa um pêndulo físico, podendo assumir qualquer forma 1D, 2D ou 3D, caracterizada por sua distribuição de massa,
\mu = \frac{dm}{dl} \\
.\\
\sigma=\frac{dm}{dA} \\
.\\
\rho=\frac{dm}{dV}e por seu momento de inércia , definido por
I=\int r^2dm
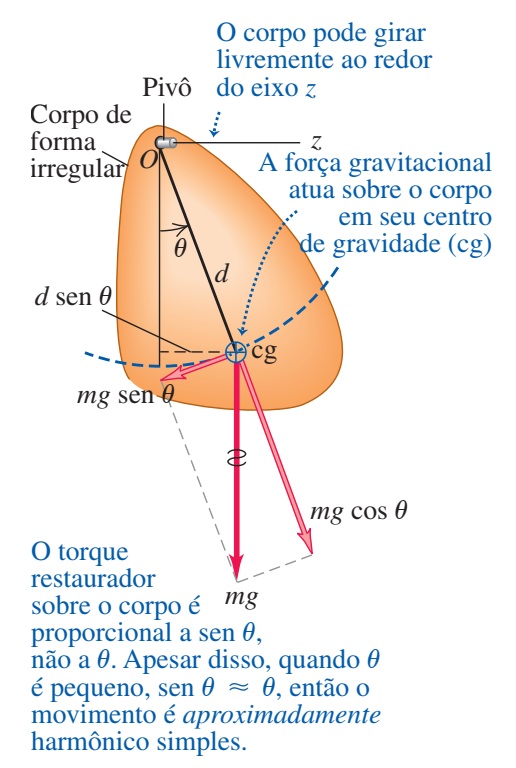
O corpo pode oscilar livremente ao redor do eixo z e está fixo pelo pivô mostrado na figura, a força peso atua no centro de gravidade (cg) do corpo, que fica localizado logo abaixo do pivô quando o corpo está parado na posição de equilíbrio, localizado a uma distância d do pivô. Deslocando-se o corpo ligeiramente de , nota-se que a única força responsável por fazer o objeto retornar a posição de equilíbrio é o peso , atuando como uma força restauradora, logo o torque resultante sobre o corpo é
\vec{\tau}_{R}=-\vec{r} \times \vec{F}onde o módulo do torque resultante é
\tau_{R}=-mgd\sin{\theta}considerando que o torque resultante é , tem-se
I \alpha_{z}=-mgd\sin{\theta}Para pequenas vibrações e considerando que ,
\frac{d^2\theta}{dt^2}+\left( \frac{mgd}{I}\right)\theta=0portanto, a frequência angular do pêndulo físico é dada por
\omega=\sqrt{\frac{mgd}{I}}Para ilustrar o comportamento de um pêndulo físico, consideremos uma régua muito fina de um metro de comprimento L = 1m e massa distribuída uniformemente, ocupando apenas um espaço 1D, como na figura (a), e um pêndulo simples de comprimento e massa m figura (b).
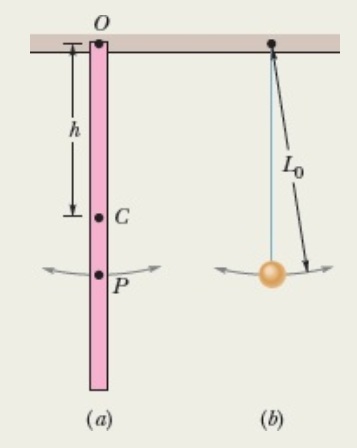
Sabendo-se que a régua pode oscilar livremente sobre o pivô no ponto O e que seu centro de gravidade coincide com o seu centro de massa em C, e que o momento de inércia da barra girando em torno do ponto O na sua extremidade é , e como , tem-se
\omega=\sqrt{\frac{mgd}{I}}=\sqrt{\frac{mg\frac{L}{2}}{\frac{mL^2}{3}}}=\sqrt{\frac{3g}{2L}}assim, o período de oscilação do pêndulo físico será
T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{2L}{3g}}=1,64sPara que o pêndulo simples da figura (b) oscile com o mesmo período encontrado acima, teremos que
T=2\pi\sqrt{\frac{L_{0}}{g}}=2\pi\sqrt{\frac{2L}{3g}} \\
ou \quad seja\\
L_{0}=\frac{2}{3}L=66,7cmBIBLIOGRAFIA
- RESNICK, Robert, HALLIDAY, David & WALKER, Jearl. FUNDAMENTOS DE FÍSICA: Gravitação, Ondas e Termodinâmica, Volume 2, 6a Edição. Rio de Janeiro: LTC, 2002.
- NUSSENZVEIG, H.M. – CURSO DE FÍSICA BÁSICA, VOL 2, ED. EDGARD BLÜCHER LTDA.
- SERWAY, Raymond A., & JEWETT Jr, John W. PRINCÍPIOS DE FÍSICA: Movimento Ondulatório e Termodinâmica, Volume 2, 3ª Edição. São Paulo: Cengage Learning, 2008.
- TIPLER, Paul A. & MOSCA, Gene. FÍSICA: Mecânica, Oscilações e Ondas, Termodinâmica, Volume 1, 5ª Edição. Rio de Janeiro: LTC, 2006.
- SEARS, Francis W. & ZEMANSKY, Mark W.; YOUNG, Hugh D. & FREEDMAN, Roger A. FÍSICA II: Termodinâmica e Ondas, 12ª Edição. São Paulo: Pearson Education.

