A Dinâmica é a parte da Mecânica que relaciona o movimento com sua causas. A dinâmica tem como base as três Leis de Newton do movimento.
O movimento de uma partícula é sempre relativo à algum referencial, ou seja, a partícula pode ter simultaneamente diferentes movimentos em relação a diferentes referenciais.
Quando uma partícula está infinitamente distante de todos os outros corpos do universo dizemos que esta é uma partícula isolada.
Referencial inercial é um referencial em relação ao qual são nulas as acelerações de uma trinca de partículas isoladas não-colineares, isto é, que não estão ao longo de uma mesma reta, quando essa regra não é obedecida o referencial é chamado não-inercial.
Sempre que usarmos um referencial terrestre, estará implícito que ele pode ser considerado inercial, a menos que seja explicitamente dito o contrário.
Qualquer referencial que se mova em MRU em relac¸ao a um referencial inercial e também um referencial inercial.
Primeira Lei de Newton
Toda partícula permanece em estado de repouso ou de movimento retilíneo uniforme, a menos que seja acelerada por forças exercidas sobre ela.

SEGUNDA LEI DE NEWTON
O produto da massa pela aceleração de uma partícula e igual à força resultante exercida sobre ela.
A força resultante é a soma vetorial de todas as forças que atuam sobre o objeto estudado, este é o princípio da superposição das forças. Digamos que há N forças atuando sobre o corpo de massa m, assim, a força resultante sobre m será
Podemos escrever a força resultante na forma de suas componentes
A massa inercial é definida pela lei das acelerações das partículas de um par isolado que diz que em um par isolado de partículas, o produto da massa pela aceleração de uma das partículas tem sempre a mesma direção, o mesmo módulo e sentido oposto ao produto da massa pela aceleração da outra partícula.
aqui i e j são as partículas isoladas que formam o par.
assim,
A equação acima nos informa que quanto maior a massa de uma partícula, menor será sua aceleração. Diz-se que quanto maior é a massa de uma partícula, maior é a dificuldade de acelerá-la.
A massa é dada em kg, no SI.
A força para Newton: “Uma força imprimida é uma ação exercida sobre um corpo a fim de alterar seu estado, seja de repouso, ou de movimento uniforme em linha reta”.
TERCEIRA LEI DE NEWTON
Se é a força sobre uma par´ticula i exercida por uma partícula j e
é a força sobre a partícula j exercida pela partícula i, então
isto é, as duas forças têm o mesmo módula, a mesma direção e sentidos opostos.
As duas forças e
são chamadas forças de ação e reação. Em outras palavras, dizemos que as forças são sempre criadas aos pares.
O problema fundamental da Mecânica Clássica diz que dadas as forças que agem sobre uma partícula, bem como sua posição e sua velocidade em um dado instante, é possível determinar o seu movimento?
A Segunda Lei de Newton e uma equação diferencial de segunda ordem, cujas soluções são os movimentos possíveis de uma partícula em um dado problema.
Princípio da Existencia e Unicidade das soluções do problema fundamental da Mecânica Clássica diz que, se forem dadas as forças sobre a partícula, a Segunda Lei de Newton determina, para essa partícula, apenas um movimento que satisfaz as condições iniciais dadas por uma posição e uma velocidade predeterminadas em algum instante fixo.
SI é o sistema internacional de unidades e medidas, CGS é a sigla para centímetro, grama e segundo e 1 slug = 14,5939 kg.
O peso de um corpo é o módulo da força para cima necessária para equilibrar a força gravitacional a que o corpo está sujeito.
A força normal é a força exercida sobre um corpo pela superfície na qual o corpo está apoiado. A força normal é sempre perpendicular à superfície.
A força de atrito é a força exercida sobre um corpo quando o corpo desliza ou tenta deslizar em uma superfície. A força é sempre paralela à superfície e tem o sentido oposto ao do deslizamento. Em uma superfície ideal, a força de atrito é desprezível.
O diagrama de corpo livre é um diagrama simplificado no qual apenas um corpo é analisado. Esse corpo é representado por um ponto ou por um desenho. Todas as forças externas que agem sobre o corpo são representadas por vetores, e um sistema de coordenadas é superposto ao desenho, escolhido de modo a simplificar a solução.
play_circle_outline
play_circle_outline
APLICAÇÕES
play_circle_outlineplay_circle_outline
play_circle_outline
Forças básicas da natureza
Sabe-se que é possível reduzir todos os tipos de forças conhecidas a apenas quatro tipos de interações fundamentais, que serão descritas a seguir.
looks_one Interações gravitacionais: que é a interação entre dois corpos de massas m1 e m2 cuja distância entre as partículas é dada por r12
looks_two Interações eletromagnéticas: Lei de Coulomb, obtida em 1785, estabelece a interação entre duas cargas elétricas q1 e q2 cuja distância entre as cargas é dada por r12
looks_3 Interações fortes: São as interações responsáveis pelas forças nucleares. O núcleo atômico é formado por prótons e nêutrons, cujas dimensões são da ordem de . A força de repulsão coulombiana entre os prótons à distâncias tão pequenas é muito grande, no entanto, temos núcleos atômicos estáveis. Logo, as interações fortes são muito maiores que as interações coulombianas. As interações fortes atuam apenas entre hádrons, que possuem a “carga hadrônica” e são os nêutrons e prótons, no núcleo atômico, e os mésons. Esse fenômeno, de escala nuclear, é tratado pela mecânica quântica.
looks_4 Interações fracas: Atuam somente na escala nuclear. As interações fracas são responsáveis pela “desintegração beta”, a emissão de elétrons pelos núcleos de certas substâncias radioativas.
Força Elástica
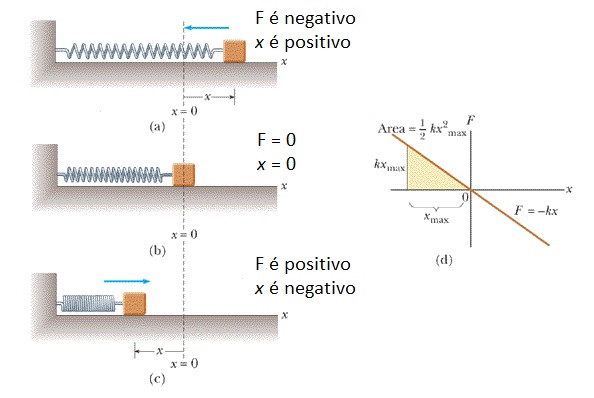
Na figura abaixo, em (b), temos uma mola no estado relaxado, ou seja, nem comprimida nem alongada. Uma das extremidades está fixa, e um objeto que se comporta como uma partícula, um bloco, por exemplo, está preso na outra extremidade. Se alongamos a mola puxando o bloco para a direita, como em (a), a mola puxa o bloco para a esquerda. Como a força elástica tende a restaurar o estado relaxado, ela também é chamada de força restauradora. Se comprimimos a mola empurrando o bloco para a esquerda, como em (c), a mola empurra o bloco para a direita.
Para x pequeno, verifica-se experimentalmente que vale a Lei de Hooke
a força restauradora é proporcional ao deslocamento medido em relação ao ponto onde a mola encontra-se relaxada, a contante de proporcionalidade k é característica da mola, também chamada de constante da mola. A lei de Hooke deixa de valer se a deformação da mola é muito grande. Veremos que a área em destaque na figura (d) é a energia potencial elástica da mola. A força elástica é resultado de forças interatômicas.
play_circle_outline
Força de Atrito
A experiência mostra que, quando um corpo seco não lubrificado pressiona uma superfície nas mesmas condições e uma força tenta fazer o corpo deslizar ao longo da superfície, a força de atrito resultante apresenta três propriedades básicas:
filter_1 Se o corpo não se move, a chamada força de atrito estático e a componente paralela à superfície se equilibram. As duas forças têm módulos iguais e
tem o sentido oposto ao da componente paralela à superfície.
em que é o coeficiente de atrito estático e N é o módulo da força normal que a superfície exerce sobre o corpo. Se o módulo da componente de F paralela à superfície excede
o corpo começa a deslizar na superfície.
filter_3 Se o corpo começa a deslizar na superfície, o módulo da força de atrito diminui rapidamente para um valor dado por
em que é o coeficiente de atrito cinético. Daí em diante, então, durante o deslizamento, uma força de atrito cinético
se opõe ao movimento.
play_circle_outline
play_circle_outline
play_circle_outline
AS LEIS DE NEWTON E O MCU
Um corpo de massa m está preso a um fio, inextensível e de peso desprezível, e gira num plano horizontal constituindo um pêndulo cônico. Sendo L o comprimento do fio, θ o ângulo que o fio forma com a vertical e g a aceleração local da gravidade, é possível determinarmos a tensão (T) no fio, a velocidade angular ω de rotação e o período τ das oscilações.
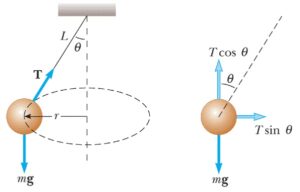
Como podemos perceber na figura, as forças que atuam sobre a partícula de massa m são o peso e a tração no fio, pela segunda Lei de Newton temos,
onde e
.
Dividindo-se uma euqção pela outra encontramos
Pela figura, vemos que o raio da trajetória é dado por
o que nos dá, para a velocidade angular da partícula
Se considerarmos que
O período do movimento é dado por
Para o saco da velocidade da partícula, temos
BIBLIOGRAFIA
HIBBELER, R. C. Dinâmica: Mecânica para Engenharia. Edição: 12 ed. São Paulo (SP): Pearson Universidades, 2010.
NUSSENZVEIG, H. M. Curso de Física Básica: Mecânica. Edição: 5 ed. [s.l.] Blucher, 2013.
RESNICK, R.; WALKER, J.; HALLIDAY, D. Fundamentos de Física – Volume 1 – Mecânica. Edição: 10 ed. [s.l.] LTC, 2016.
SERWAY, R.; JEWETT, J. Princípios de física – vol. I: Volume 1. Edição: 2 ed. [s.l.] Cengage Learning, 2014.
YOUNG, H. D.; FREEDMAN, R. A. Física de Sears & Zemansky: Volume I: Mecânica: Volume 1. Edição: 14 ed. [s.l.] Pearson Universidades, 2015.

