O famoso jogo de petecas, que é jogado com diversos participantes, cada um com um conjunto de esferas de vidro ou de aço, “as bolinhas”, travam uma batalha para “zerar” os adversários, conquistando cada uma de suas bolinhas, através das diversas modalidades do jogo, tais como, o turiti, a honda, ou o mata-mata.
O que esse jogo infantil tem a ver com um dos princípios de conservação mais importante da Física? Em uma das modalidades o jogador deve fazer sua bolinha colidir com, pelo menos, duas outras, para vencer a jogada, ou lançar sua bolinha no círculo, onde as bolinhas da rodada são “casadas”, postas para que o jogador possa retirá-las com seu lance. Por que as bolinhas são removidas da honda, ou por que após colidir com a primeira, ainda possui movimento para atingir a próxima, percorrendo até uma direção diferente da direção do lançamento inicial?
O conceito de momento linear ou quantidade de movimento explicará o por quê, quando analisarmos o comportamento dessas partículas circunscritas, que entram em colisão umas com as outras, após de lançamento da “ponteira”, bolinha que o jogador usa para fazer as jogadas. Qualquer curumim, conhece intuitivamente, o que ocorre com as bolinhas durante a colisão, sabem, inclusive, como lança-la para que a mesma, atingindo as demais, possa torna-lo o vencedor.
Momento Linear de uma Partícula e sua Conservação
Newton definiu o momento linear de um corpo com massa m que se movimenta com uma velocidade , hoje utilizamos a forma vetorial descrita a seguir:
A segunda lei de Newton pode ser escrita na forma da taxa de variação temporal do momento linear
onde é a força resultante que atua sobre a partícula de massa m, assumindo a mesma orientação da taxa de variação temporal do momento linear.
Consideremos duas bolinhas do jogo de petecas, podemos escrever a equação de movimento para cada uma das bolinhas e, levemos em conta que elas estão na iminência da colisão. Durante a colisão as forças que podem atuar sobre as bolinhas são as forças de contato da colisão e
, devido a terceira lei de Newton e, as forças externas resultantes que atuam sobre cada uma das bolinhas do problema são
e
, onde os índices 1 e 2, representam as partículas envolvidas na colisão, teremos
como podemos perceber e
, são os momentos lineares das partículas 1 e 2, respectivamente. Se considerarmos que apenas estas duas bolinhas colidem podemos determinar o momento linear total
do sistema, o que nos dá
a taxa de variação temporal do momento linear total do sistema é a soma vetorial das taxas de variação temporal dos momentos de cada partícula, temos
como estamos considerando forças internas newtonianas, , e considerando a força externa total do sistema como sendo a soma das forças externas que atuam em cada partícula
, podemos concluir que a condição necessária e suficiente para que o momento linear seja conservado, para este problema de duas partículas, é que a força externa total do sistema deve ser nula, o que nos leva a crer que as forças externas resultantes que atuam sobre cada partícula são nulas ou possuem o mesmo módulo, a mesma direção e sentidos opostos, logo
Centro de Massa de um Sistema de Partículas
A equação anterior sugere que podemos descrever o movimento das duas partículas se movendo, como se fosse o problema de uma partícula de momento linear sobre a ação de forças externas
.
Dessa maneira podemos escrever
Se considerarmos que é possível expressar o movimento destas duas partículas por um ponto que represente toda a massa do sistema, onde
e a velocidade deste ponto, chamada Vetor Velocidade do Centro de Massa é definida como
logo,
Pode-se definir a posição do centro de massa por maio da expressão
Assim, como as massas são constantes
portanto, por identidade, a Vetor Posição do Centro de Massa é
o vetor posição do centro de massa escrito em termos de suas componentes, com vetores de base canônicos é
, com
A equação acima vale para um sistema com duas partículas.
Analisemos um pouco mais as características do centro de massa, para isso consideremos a figura, onde é o vetor posição do centro de massa,
é o vetor posição da partícula 1,
é o vetor posição da partícula 2, todos em relação ao referencial inercial em repouso O, entretanto, os vetores
e
, que são os vetores que localizam as partículas 1 e 2, respectivamente, são escritos em relação à posição do centro de massa do sistema.
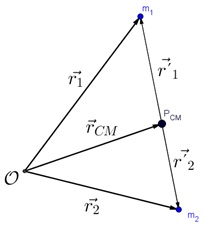
Vemos que a relação entre os vetores é dada por
Substituindo a equação do vetor posição do centro de massa, obtemos
com um pouco de álgebra, escrevemos
obtemos, após simplificações
o que dá
este resultado indica que e
são vetores com sentidos opostos, ou seja, são antiparalelos e, o centro de massa é um ponto do segmento de reta formado pelos pontos que localizam m1 e m2.
No caso particular, onde as massas são iguais, o centro de massa será encontrado no ponto médio do segmento de reta que une as partículas.
Outro ponto importante associado a equação acima é o fato de que o momento linear total do sistema em relação ao centro de massa é nulo, significando que o momento linear total do sistema se concentra no movimento do centro de massa.
Consideremos um sistema sendo formado por N partículas, cujas massas são m1, m2, m3,…, mN, com vetores posição num dado instante t, dados por , respectivamente. Qualquer partícula do sistema está sujeita a forças internas e forças externas, podemos então, dizer que a partícula i-ésima está sujeita as forças internas
e forças externa , portanto, , pois apenas forças internas newtonianas são consideradas e com (i,j = 1,2,3,…,N).
As equações de movimento do sistema de partículas podem ser escritas na seguinte forma abreviada,
a soma dupla sobre as forças internas newtonianas é nula, a restrição é importante para que não somemos duas vezes a mesma interação dos pares ação-reação, restando a equação
o momento linear total o sistema será conservado se a soma das forças externa for nula, teremos
que é o vetor velocidade do centro de massa de sistema de N partículas e,
o vetor posição do centro de massa de sistema de N partículas.
Imaginemos um corpo de massa M, com distribuição contínua de matéria, e consideremos que a massa total deste corpo ocupa um volume total ΔV, de forma que este corpo pode ser decomposto em um número finito de porções de massa Δmi, que ocupam um volume ΔVi, de forma que tenhamos e que
. Tomando-se um ΔVi suficientemente pequeno, podemos dizer que a massa Δmi é uma espécie de “partícula puntiforme” que forma o corpo de massa M, localizada pelo vetor posição
, assim o centro de massa deste corpo pode ser determinado pela expressão
onde é o vetor posição do centro de massa do corpo de massa M, no entanto, se tomarmos o limite das somas com
, teremos
com o denomidador da fração igual a massa total do corpo M.
Podemos utilizar o conceito de densidade volumétrica de massa , fazendo ΔVi um pequeno volume em torno do ponto e Δmi a massa correspondente, logo
teremos ainda, a densidade superficial de massa, tal que
onde ΔSi é uma pequena área em torno do ponto e Δmi a massa correspondente e, a densidade linear de massa
onde Δli é um pequeno comprimento em torno do ponto e Δmi a massa correspondente.
Impulso de uma Força e Momento Linear
As forças de contato, ou forças impulsivas, atuam durante um curto intervalo de tempo e seu máximo tem um elevado módulo. A colisão entre o pé de um jogador de futebol e uma bola, são exemplos desta força. Sabe-se que há outras forças atuando sobre a bola de futebol, como a gravidade e a resistência do ar, no entanto, durante a colisão, a força impulsiva é muito maior que as demais, de forma que podemos desprezar as influências destas últimas.
Definiremos colisão como sendo um evento de curta duração entre dois corpos, originado por forças impulsivas, que alteram seus movimentos, promovendo, ou não, trocar energia e momento linear, e que não necessariamente há contato entre os corpos interagentes.
Durante o intervalo , em que a força impulsiva
atua, esta força é a dominante, como no exemplo do jogador de futebol chutando a bola. Dizemos, então, que a força
é a força resultante, e pela segunda lei de Newton, temos
onde é o vetor momento linear da partícula de massa m, que pode ser a bola do exemplo, considerando-a uma partícula puntiforme.
Integrando ambos os lados da equação , teremos
chamaremos de impulso a integral da força impulsiva aplicada a uma partícula durante o intervalo de tempo
. Como podemos ver, o impulso de uma força é igual a variação do momento linear da partícula
este resultado é conhecido como o teorema do impulso e variação do momento linear.
Se conhecermos a forma como a força impulsiva varia, podemos calcular o impulso integrando-a no intervalo de tempo
, que é o mesmo que calcular a área entre a curva e o eixo do tempo t, devemos aqui entender que como a força impulsiva é um vetor, preciso é calcular o impulso para cada componente da força impulsiva. Em muitas situações não sabemos como a força impulsiva varia, podemos utilizar o valor médio da força impulsiva, que é dada por
Se analisarmos o outro corpo envolvido na colisão, verificamos que o impulso tem o mesmo módulo, a mesma direção e sentido oposto. Significa que o impulso experimentado pelo pé do jogador tem sentido oposto ao da experimentado pela bola.
BIBLIOGRAFIA
HIBBELER, R. C. Dinâmica: Mecânica para Engenharia. Edição: 12 ed. São Paulo (SP): Pearson Universidades, 2010.
NUSSENZVEIG, H. M. Curso de Física Básica: Mecânica. Edição: 5 ed. [s.l.] Blucher, 2013.
RESNICK, R.; WALKER, J.; HALLIDAY, D. Fundamentos de Física – Volume 1 – Mecânica. Edição: 10 ed. [s.l.] LTC, 2016.
SERWAY, R.; JEWETT, J. Princípios de física – vol. I: Volume 1. Edição: 2 ed. [s.l.] Cengage Learning, 2014.
YOUNG, H. D.; FREEDMAN, R. A. Física de Sears & Zemansky: Volume I: Mecânica: Volume 1. Edição: 14 ed. [s.l.] Pearson Universidades, 2015.

