Considere duas partículas colidindo unidimensionalmente.
As partículas m1 com velocidade inicial v1i e a partícula m2 com velocidade inicial v2i, colidem unidimensionalmente, se a colisão for inelástica, considere que o coeficiente de restituição e varia no intervalo de 0 a 1, onde, e = 0 é uma colisão completamente inelástica e e = 1 um colisão perfeitamente elástica. Após a colisão, as partículas assumem as velocidades v1f para a partícula de massa m1 e v2f para a partícula de massa m2.
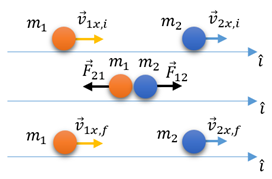
Colisões Elástica e Inelástica 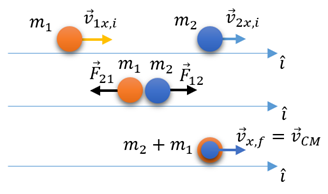
Colisão Completamente Inelástica
Mostre que as velocidades finais das partículas m1 e m2 , após a colisão, são determinadas por
onde e é o coeficiente de restituição.
INSTRUÇÕES DE CONSTRUÇÃO NO GEOGEBRA
1 – Crie o controle deslizante do tempo ;
2 – Crie o controle deslizante o coeficiente de restituição ;
3 – Crie as variáveis de massas m1 e m2 , cujos valores poderão se alterados pelo usuário;
4 – Crie as variáveis de velocidades v1i e v2i , cujos valores poderão ser alterados e tendo-se v1i > v2i como condição obrigatória para a colisão;
5 – Escreva as posições iniciais de cada partícula e as funções horárias da posição de cada partícula, antes da colisão;
6 – Calcule o instante da colisão tc , igualando as posições das partículas;
7 – Escreva as funções horárias da posição das partículas após a colisão. Lembre que as funções devem considerar a posição da colisão como a posição inicial das partículas e o cronômetro deve ser o mesmo de antes da colisão, logo
8 – Crie dois pontos A e B, que irão representar as partículas e escreva suas componentes, considere que as posições y são nulas.
9 – Monte o design da sua simulação.

