Hidrodinâmica

ESCOAMENTO DE UM FLUIDO

Um fluido ideal é um fluido incompressível, aquele cuja densidade não varia e sem nenhum atrito interno, que para fluidos é chamado de viscosidade.

A trajetória de uma partícula individual durante o escoamento de um fluido
denomina-se linha de fluxo ou linha de escoamento.

Quando a configuração global do escoamento de um fluido não varia com o tempo, ele se chama escoamento estacionário ou escoamento permanente.

Uma linha de corrente é uma curva cuja tangente em cada ponto dá a direção e o sentido da velocidade no respectivo ponto.

Pode-se caracterizar um fluido ideal por meio das seguintes propriedades;

• O fluido ideal executa um escoamento laminar, velocidade do fluido em um ponto fixo qualquer não varia com o tempo, nem em módulo nemem orientação. O escoamento é caótico ou turbulento quando a velocidade vria com o tempo e a linhas de de corrente estão desordenadas. Um importante parâmetro de estudo dos escoamentos é o Número de Reynolds.
• O fluido ideal é incompressível, sua massa específica tem um valor uniforme e constante.
• O fluido ideal é não-viscoso, considera-se um fluido viscoso quando este apresenta viscosidade que é uma medida da resistência que o fluido oferece ao escoamento.
• O fluido ideal é irrotacional, não identificaremos formação de vórtices.

EQUAÇÃO DA CONTINUIDADE

Definimos a Vazão Mássica ou fluxo de massa como sendo a taxa de variação da massa em relação ao tempo,

\dot{m} = \frac{dm}{dt}=\frac{d}{dt}(\rho V)=\rho\frac{dV}{dt}=\rho \dot{V}

\dot{m}=\rho A v

Definimos a Vazão Volumétrica ou fluxo de volume como sendo a taxa de variação do volumeem relação ao tempo,

\dot{V} = \frac{dV}{dt} = \frac{d}{dt}(Ax)=A\frac{dx}{dt}=Av

\dot{V} = Av

ESCOAMENTO EM REGIME PERMANENTE

Um escoamento em regime permanente conserva o fluxo de massa, para qualquer fluido, e conserva a fluxo de volume quando o fluido é incompressível.

\dot{m}_{entrada}=\dot{m}_{saida}

\rho_{2}A_{2}v_{2} = \rho_{1}A_{1}v_{1}

para um fluido incompressível tem-se

\dot{V}_{entrada}=\dot{V}_{saida}

A_{2}v_{2} = A_{1}v_{1}

ESCOAMENTO EM REGIME TRANSIENTE

O fluxo de massa do volume de controle é igual a diferença entre o fluxo de massa de entrada pelo fluxo de massa de saida,

\dot{m}_{VC}=\dot{m}_{entrada}-\dot{m}_{saída}

Exercício 01 – Aumente a velocidade de reprodução do vídeo

EQUAÇÃO DE BERNOULLI

De acordo com a equação da continuidade, a velocidade do escoamento de um fluido pode variar com as trajetórias desse fluido e a pressão também pode variar; ela depende da altura e também da velocidade do escoamento.

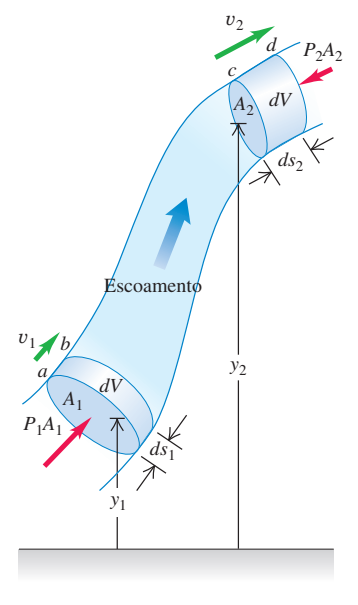
Utilizaremos o Teorema do Trabalho e da Variação da energia Cinética para determinar a equação da continuidade que considera mudanças na velocidade, na pressão e na altura.

Primeiro tomemos que o trabalho total é dado pela soma do trabalho produzido pelo fluido devido as forças de pressão W_F e pelo trabalho da força peso W_P do elemento de fluido de volume dV, e densidade ρ;

W_{total} = \Delta E_{C}

logo,

W_{F}+W_{P} = \frac{1}{2}m(v_{2}^2-v_{1}^2)

O trabalho realizado pela força peso W_P é igual a

W_{P} = \vec{P} \cdot \Delta\vec{ r} \\
W_{P} = P \Delta y \cos 180° \\
W_{P} = -mg\Delta y \\
W_{P} = - \rho g \Delta V (y_{2}-y_{1}) \\

O trabalho realizado pela força de pressão W_F é igual a

W_{F} = -F_{2} \Delta _{2}+ F_{1} \Delta x_{1} \\
W_{F} = - P_{2} A_{2} \Delta x_{2} + P_{1} A_{1} \Delta x_{1} \\
W_{F} = P_{1} \Delta V_{1} - P_{2} \Delta V_{2} \\
W_{F} = (P_{1} - P_{2}) \Delta V 

Substituindo os trabalhos encontrados na equação dao Teorema Trabalho-Energia, temos

(P_{1} - P_{2}) \Delta V  -  \rho g \Delta V (y_{2}-y_{1}) = \frac{1}{2} \rho \Delta V(v_{2}^2 - v_{1}^2 )\\

Agrupando as grandezas de mesmo índice, encontramos

P_{1} + \rho g y_{1} + \frac{1}{2} \rho v_{1}^2 = P_{2} + \rho g y_{2} + \frac{1}{2} \rho v_{2}^2

Como a equação de Bernoulli é aplicada para fluidos incompressíveis, o volume do elemento de fluido não varia, o escoamento deve ser estacionário e não deve haver viscosidade, logo

\Delta V_{1} = \Delta V_{2} = \Delta V

Exercício 02 – Aumente a velocidade de reprodução do vídeo

Exercício 03 – Aumente a velocidade de reprodução do vídeo

Exercício 04 – Aumente a velocidade de reprodução do vídeo

BIBLIOGRAFIA

• RESNICK, Robert, HALLIDAY, David & WALKER, Jearl. FUNDAMENTOS DE FÍSICA: Gravitação, Ondas e Termodinâmica, Volume 2, 6^a Edição. Rio de Janeiro: LTC, 2002.
• NUSSENZVEIG, H.M. – CURSO DE FÍSICA BÁSICA, VOL 2, ED. EDGARD BLÜCHER LTDA.
• SERWAY, Raymond A., & JEWETT Jr, John W. PRINCÍPIOS DE FÍSICA: Movimento Ondulatório e Termodinâmica, Volume 2, 3ª Edição. São Paulo: Cengage Learning, 2008.
• TIPLER, Paul A. & MOSCA, Gene. FÍSICA: Mecânica, Oscilações e Ondas, Termodinâmica, Volume 1, 5ª Edição. Rio de Janeiro: LTC, 2006.
• SEARS, Francis W. & ZEMANSKY, Mark W.; YOUNG, Hugh D. & FREEDMAN, Roger A. FÍSICA II: Termodinâmica e Ondas, 12ª Edição.  São Paulo: Pearson Education.