Simulação: Ilusão e Osciladores

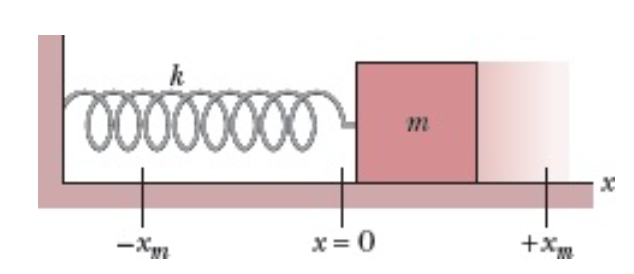
Sabe-se que o modelo mais simples de Oscilador Harmônico é o sistema massa-mola, que consiste em prender uma mola de constante elástica k em um bloco de massa m, tendo-se uma das extremidades da mola presa à parede, considerando-se que não há atrito entre o bloco e a superfície horizontal sobre a qual o sistema está montado, veja a figura 1.

Utilizando-se as Leis de Newton da Mecânica e a lei de Hooke, que descreve a força produzida por uma mola sobre um bloco de massa m, obtem-se, para o movimento ao longo da direção

F_{Rx}=F_{el}=-kx=m\frac{d^2x}{dt^2}

logo, a equação de movimento o oscilador harmônico massa-mola é

\frac{d^2x}{dt^2}+\frac{k}{m}x=0

Como sabe-se, a força elástica F_el é uma força conservativa, associando-se a ela uma energia potencial U(x) dada por:

U(x) = \frac{1}{2}kx^2

tomando-se a posição inicial de relaxamento da mola em x_i = 0, o que nos dá

F_{el}=-\frac{dU}{dx}

A Solução da equação de movimento encontrada é uma função periódica, da forma x(t) = x(t + T)

Como a oscilação iniciará na extremidade positiva do eixo x, podemos sugerir a solução sendo uma função tipo trigonométrica, logo

x(t) = x_{m} cos(wt+\theta)

onde w é a frequência angular do oscilador, dada por w = 2π/T, onde T é o período do movimento de oscilação,

x_m é amplitude de oscilação, o maior valor que x pode assumir, θ é a fase inicial e t é o tempo.

Pode-se mostrar que, se a oscilação for ao longo do eixo y, tem-se

y(t) = y_{m} sin(wt + \theta)

onde y_m é amplitude de oscilação, o maior valor que y pode assumir.

Na figura 2, pode-se observar a relação entre o Movimento Circular uniforme da partícula Q e o Movimento Harmônico Simples representado pelo ponto P que é a projeção ao longo do eixo x.

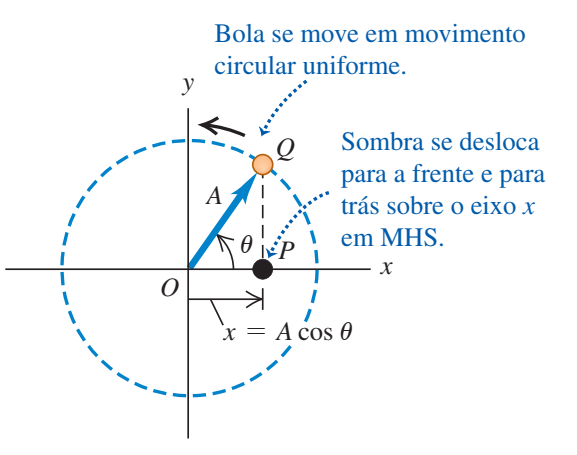
Pode-se concluir que a partícula em MCU combina os MHS de cada eixo, o que nos dá

\begin{cases}
x(t) =&A\cos(wt+\theta) \\
y(t) =&A\sin(wt+\theta)
\end{cases}

Vê-se que a partícula descreve um movimento circular com o raio da circunferência igual a A,

x^2 = A^2 \cos^2(wt+\theta)

y^2 = A^2 \sin^2(wt+\theta)

utilizando-se a identidade

\sin^2(wt+\theta)+\cos^2(wt+\theta)=1

Tem-se

x^2+y^2=A^2

Considere uma partícula em MHS movendo-se em uma reta crescente passando pela origem do sistema,

y=(\tan \phi) x

Vemos que a componente y e x devem possuir a condição

\sin \phi y = \cos \phi x

Assim, caso φ = π/4, tem-se a partícula movendo-se ao longo da reta inclinada, crescente igual a

y=(\tan \frac{\pi}{4}) x

O resultado é mostrado no video a seguir;