Trabalho e Energia

Consideremos uma partícula de massa m submetida a ação de uma força total F que é função da posição, da velocidade e do instantes de tempo em que se encontra a partícula, dessa forma a situação considerada é descrita pela expressão:

\vec{F}=f(\vec{r},\vec{v},t)=m\vec{a}

Sabe-se que quando uma força resultante é aplicada a um objeto de massa m, este altera seu estado, e essa mudça é observada em sua velocidade, que pode aumentar, diminuir ou até zerar.

Nestas alterações de estado do corpo, causadas pela ação da força, dizemos que um trabalho W é realizado pela força sobre o objeto.

TRABALHO

Trabalho W é a energia transferida para um objeto ou de um objeto por meio de uma força que age sobre o objeto. Quando a energia é transferida para o objeto, o trabalho é positivo; quando a energia é transferida do objeto, o trabalho é negativo.

O conceito de “vis viva” do corpo, como a designava Leibniz, ao produto da massa de um corpo pelo quadrado de sua velocidade, era aplicado quando um corpo estiva sujeito à ação de uma força resultante diferente de zero, o que resultava na não conservação da sua “força viva”.

Consideremos o MRUV, como sabemos uma força resultante diferente de zero atua sobre um corpo de massa m produzindo uma aceleração constante a, pela equação de Torricelli tem-se

v_{f}^{2}=v_{i}^{2}+2a\Delta s

multiplicando-se ambos os lados por m

mv_{f}^{2}=mv_{i}^{2}+2ma\Delta s

mv_{f}^{2}-mv_{i}^{2}=2ma\Delta s

mv_{f}^{2}-mv_{i}^{2}=2F\Delta s

Neste caso, há um aumento da “vis viva” ou “força viva” do corpo, que, para uma dada distância, será tanto maior quanto maior for a intensidade da força aplicada F.

Se a força resultante aplicada F for direcionada a um ângulo θ com a horizontal, a componente da força F que altera o estado do corpo é a paralela ao deslocamento, logo teríamos

mv_{f}^{2}-mv_{i}^{2}=2Fcos\theta \Delta s

Por outro lado, se a força resultante aplicada fosse ocasionada pelo atrito, a partícula iria parar após percorrer a distância Δs, consequentemente tería-se a total transformação da “vis viva” original em “vis mortae”.

No período compreendido entre 1819 a 1839, através de obras como as de Gustave Coriolis (1792-1843), Jean Poncelet (1788-1867) e Claude Navier (1785-1836), entre outros, com temas centrais de estudo versando sobre a análise de máquinas em movimento, que o conceito de trabalho mecânico se estabelece, definitivamente. O resultado disto é a definição da energia cinética de uma partícula

E_{c}=\frac{1}{2}mv^2

O que nos dá, pelas equações obtidas acima

E_{cf}-E_{ci}=F_{R}cos\theta \Delta s

\Delta E_{c}=W

Para calcular o trabalho que uma força realiza sobre um objeto quando este sofre um deslocamento, usamos apenas a componente da força paralela ao deslocamento do objeto. A componente da força perpendicular ao deslocamento não realiza trabalho.

O trabalho realizado por uma força é positivo, se a força possui uma componente vetorial no sentido do deslocamento, e negativo, se a força possui uma componente vetorial no sentido oposto. Se a força não possui uma componente vetorial na direção do deslocamento, o trabalho é nulo.

Com o avanço da Matemática e dos conceitos físicos o trabalho passou a ser definido como

W=\int\vec{F} \sdot d \vec{r}

O PRODUTO INTERNO OU PRODUTO ESCALAR

Devemos discutir um pouco sobre o produto interno entre dois vetores quaisquer, para isso, consideremos os vetores $\vec{r}_{1}=x_1\hat{i}+y_1\hat{j}+z_1\hat{k}$ e $\vec{r}_{2}=x_2\hat{i}+y_2\hat{j}+z_2\hat{k}$ , escritos em termos dos vetores canônicos $\left \{ \hat{i},\hat{j},\hat{k} \right \}$ , com módulos $\left | \vec{r}_1 \right |=\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}$ e $\left | \vec{r}_2 \right |=\sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}$ , sabendo que o ângulo θ é o ângulo formado entre os vetores $\vec{r}_1$ e $\vec{r}_2$ , quando estes compartilham a mesma origem, tem-se

\vec{r}_{1} \sdot \vec{r}_{2}= |\vec{r}_{1}||\vec{r}_{2}|\cos \theta

ou seja, o produto interno é o número obtido quando multiplicamos o módulo do primeiro vetor pelo módulo do segundo vetor pelo cosseno do ângulo formado entre os vetores envolvidos no produto.

A definição acima nos leva a considerar os produtos entre os vetores canônicos $\left \{ \hat{i},\hat{j},\hat{k} \right \}$ , como todos são vetores ortogonais entre si, teremos

\begin{cases} \hat{i} \sdot \hat{i}=\hat{j} \sdot \hat{j}=\hat{k} \sdot \hat{k}=1 \\ \hat{i} \sdot \hat{j}=\hat{j} \sdot \hat{i}=0 \\ \hat{i} \sdot \hat{k}=\hat{k} \sdot \hat{i}=0 \\ \hat{j} \sdot \hat{k}=\hat{k} \sdot \hat{j}=0 \end{cases}

O produto escalar possui as seguintes propriedades:

O produto escalar entre dois vetores não depende da ordem for fatores, ou seja, o produto é comutativo.

\vec{r}_{1} \sdot \vec{r}_{2}=\vec{r}_{2} \sdot \vec{r}_{1}

O produto escalar de vetores é distributivo em relação à soma de vetores.

(\vec{r}_{1} +\vec{r}_{2}) \sdot \vec{r}_{3}=\vec{r}_{1} \sdot \vec{r}_{3}+\vec{r}_{2} \sdot \vec{r}_{3}

Quando um dos vetores do produto escalar é multiplicado por um escalar (número), o produto fica multiplicado por este escalar (número).

(\alpha \vec{r}_{1}) \sdot \vec{r}_{2}=\vec{r}_{1} \sdot (\alpha \vec{r}_{2})=\alpha (\vec{r}_{1} \sdot \vec{r}_{2})

A derivada do produto escalar entre dois vetores é igual ao produto escalar da derivada do primeiro vetor pelo segundo vetor somado pelo produto escalar entre o primeiro vetor e a derivada do segundo vetor.

\frac{d}{dt}(\vec{r}_{1} \sdot \vec{r}_{2})= \frac{d\vec{r}_{1}}{dt} \sdot \vec{r}_{2}+\vec{r}_{1} \sdot \frac{d\vec{r}_{2}}{dt}

Utilizando as relações acima e as propriedades do produto escalar, podemos realizar o produto escalar entre dois vetores como se segue;

\vec{r}_{1} \sdot \vec{r}_{2}=(x_{1}\hat{i}+y_{1}\hat{j}+z_{1}\hat{k}) \sdot (x_{2}\hat{i}+y_{2}\hat{j}+z_{2}\hat{k})

aplicando-se a propriedade distributiva, tem-se

\begin{array}{cc} \vec{r}_{1} \sdot \vec{r}_{2}= & x_{1}x_{2} \underbrace{(\hat{i} \sdot \hat{i})}_{\text{=1}}+& x_{1}y_{2} \underbrace{(\hat{i} \sdot \hat{j})}_{\text{=0}}+ & x_{1}z_{2} \underbrace{(\hat{i} \sdot \hat{k})}_{\text{=0}}+ \\ & y_{1}x_{2} \underbrace{(\hat{j} \sdot \hat{i})}_{\text{=0}}+ & y_{1}y_{2} \underbrace{(\hat{j} \sdot \hat{j})}_{\text{=1}}+ & y_{1}z_{2} \underbrace{(\hat{j} \sdot \hat{k})}_{\text{=0}}+ \\ & z_{1}x_{2} \underbrace{(\hat{k} \sdot \hat{i})}_{\text{=0}}+ & z_{1}y_{2} \underbrace{(\hat{k} \sdot \hat{j})}_{\text{=0}}+ & z_{1}z_{2} \underbrace{(\hat{k} \sdot \hat{k})}_{\text{=1}} \\ \end{array}

portanto,

\vec{r}_{1} \sdot \vec{r}_{2}=x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}

Para encontrarmos o trabalho realizado pela força resultante, fazemos

W=\int{\vec{F}_{R}\sdot d\vec{r}}=\int{\sum_{i=0}^{N}{\vec{F}_{i}\sdot d\vec{r}}}

W=\int{\vec{F}_{1} \sdot d\vec{r}}+\int{\vec{F}_{2} \sdot d\vec{r}}+\cdots+\int{\vec{F}_{N} \sdot d\vec{r}}

ou seja,

W=W_{1}+W_{2}+ \cdots+W_{N}

Conclui-se que o trabalho total realizado sobre uma partícula de massa m é a soma dos trabalhos de cada força que atua sobre a partícula, portanto é o trabalho da força resultante.

W_{T}=\sum_{i=1}^{N}{W_{i}}=\int{\vec{F}_{R} \sdot d\vec{r}}

A unidade SI de trabalho é o joule (J), nome dao em homenagem ao físico inglês do século XIX James Prescott Joule.

1 J=1N.m=1kg.m^2.s^{-2}

TRABALHO REALIZADO PELA FORÇA GRAVITACIONAL

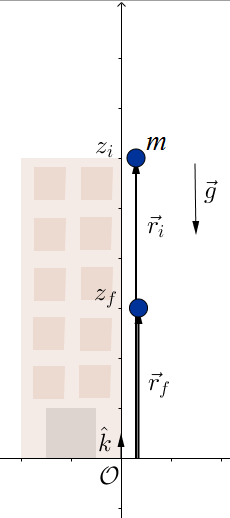
Dizemos que toda força tem capacidade de produzir um deslocamento quando atua sobre um corpo de massa m, se considerarmos, no caso do corpo abandonado próximo à superfície terrestre, este partindo do repouso, ainda, considerando um referencial inercial no solo, e este caindo sem a influência da resistência do ar, figura abaixo, teremos o vetor posição inicial do corpo puntiforme dado por $\vec{r}_{i}=z_i \hat{k}$ e o vetor posição final $\vec{r}_{f}=z_f \hat{k}$ , com $z_f<z_i$ , a força gravitacional que atua sobre o corpo puntiforme dado por $\vec{F}_{g}=-mg\hat{k}$ , onde g é a aceleração da gravidade terrestre, e o vetor deslocamento será $\Delta \vec{r}=-|(z_f-z_i)|\hat{k}$ . A variação da velocidade da partícula, sabendo que a aceleração da g gravidade terrestre, nestas condições pode ser considerada constante, será $\Delta \vec{v}=-\sqrt{2g|(z_f-z_i)|}\hat{k}$ , podemos definir o trabalho realizado por uma força constante como sendo

W=\int{\vec{F}_{g} \sdot d\vec{r}}=\vec{F}_{g}\sdot \int{d\vec{r}}=\vec{F}_{g} \sdot \Delta \vec{r}

substituindo os valores , e como a força gravitacional é constante, temos

W=\left( -mg\hat { k } \right) \sdot \left( -|{ z }_{ f }-{ z }_{ i }|\hat { k } \right)

W=mg|z_f-z_i|

Se considerarmos a força gravitacional como

\vec{F}_{g}=G\frac{m_1m_2}{r^2}\hat{r}

O trabalho será

W=\int{\vec{F}_{g}\sdot d\vec{r}}=\int_{r1}^{r2}{G\frac{m_1m_2}{r^2}dr}

W=Gm_1m_2\int_{r_1}^{r_2}{\frac{dr}{r^2}}=Gm_1m_2\left[ \frac{r^{-2+1}}{-2+1} \right]_{r1}^{r2}

W=-Gm_1m_2\left( \frac{1}{r_2}-\frac{1}{r_1} \right)

Podemos perceber os valores de $r_1$ e $r_2$ irão definir o sinal do trabalho.

TRABALHO REALIZADO PELA FORÇA ELÁSTICA

Considerando que a força exercida pela mola sobre um bloco de massa m é dada pela lei de Hooke

\vec{F}_{e}=-k\Delta \vec{r}

onde k é a constante elástica da mola, um número positivo, e $\Delta \vec{r}$ o vetor deslocamento produzido sobre a mola.

Para simplificar nosso cálculos tomaremos apenas o deslocamento na direção x, assim, o trabalho realizado pela mola sobre o bloco, quando este é puxado distendendo a mola, fica

W=\int_{x_1}^{x_2}{(-F_{ex}\hat{i}) \sdot (dx \hat{i})}=\int_{x_1}^{x_2}{(-kxdx)}\underbrace{(\hat{i} \sdot \hat{i})}_{\text{=1}}

W=-k \left[ \frac{x^{1+1}}{1+1} \right]_{x_1}^{x_2}=-\frac{1}{2}k\left( x_{2}^{2}-x_{1}^{2} \right)

Se a mola é esticada, então x é positivo e a componente da força elástica é negativa. Se a mola é comprimida, então x é negativo e a componente da força elástica é positiva.

W=-\left( \frac{1}{2}kx_{2}^{2}- \frac{1}{2}kx_{1}^{2} \right)

FORÇAS CONSERVATIVAS E NÃO-CONSERVATIVAS

Uma força cujo trabalho, em qualquer deslocamento, depende apenas dos pontos inicial e final do deslocamento é chamada força conservativa, ou ainda, forças conservativas são aquelas que realizam o mesmo trabalho para qualquer caminho possível entre dois pontos.

Listaremos três propriedades das forças conservativas;

O trabalho deve ser aditivo.

W(x_1,x_3)=W(x_1,x_2) + W(x_2,x_3)

O trabalho em um circuito fechado é nulo.

W(x_1,x_1)=0

W(x_1,x_2)=-W(x_2,x_1)

As forcas que não são conservativas violam essas propriedades.

Denominamos força não-conservativa a força que não é conservativa e dizemos que ela é dissipativa no caso em que é negativo o trabalho que realiza em caminhos fechados ou em qualquer caminho relevante no movimento em tela.

POTÊNCIA

A taxa de variação com o tempo do trabalho realizado por uma força recebe o nome de potência.

A potência instantânea P é a taxa de variação instantânea com a qual o trabalho é realizado e é definida como

P=\frac{dW}{dt}

A potência média desenvolvida durante um intervalo de tempo Δt, de uma força que realiza um trabalho W é

P_{med}=\frac{W}{\Delta t}

Também podemos expressar a taxa com a qual uma força realiza trabalho sobre uma partícula, ou um objeto que se comporta como uma partícula, em termos da força e da velocidade da partícula.

P=\frac{dW}{dt}=\frac{\vec{F} \sdot d\vec{r}}{dt}=\vec{F} \sdot \frac{ d\vec{r}}{dt}

P=\vec{F} \sdot \vec{v}

A unidade de potência do SI é o joule por segundo. Essa unidade é usada com tanta frequência que recebeu um nome especial, o watt (W), em homenagem a James Watt, cuja contribuição foi fundamental para o aumento da potência das máquinas a vapor.

1 watt=1W=1J/s=0,738 ft.lb/s

1 hp = 745,7W \\ 1cv=735,5W

APLICAÇÕES

REFERÊNCIAS

HIBBELER, R. C. Dinâmica: Mecânica para Engenharia. Edição: 12 ed. São Paulo (SP): Pearson Universidades, 2010.

NUSSENZVEIG, H. M. Curso de Física Básica: Mecânica. Edição: 5 ed. São Paulo – SP: Blucher, 2013.

PEDUZZI, L. O. Q.; PEDUZZI, S. S. Física Básica B. 2^a ed. Florianópolis – SC: Universidade Federal de Santa Catarina/CFM/CED/UFSC, 2010.

RESNICK, R.; WALKER, J.; HALLIDAY, D. Fundamentos de Física – Volume 1 – Mecânica. Edição: 10 ed. Rio de Janeiro – RJ: LTC, 2016.

SERWAY, R.; JEWETT, J. Princípios de física – vol. I: Volume 1. Edição: 2 ed. São Paulo-SP. Cengage Learning, 2014.

YOUNG, H. D.; FREEDMAN, R. A. Física de Sears & Zemansky: Volume I: Mecânica: Volume 1. Edição: 14 ed. São Paulo – SP: Pearson Universidades, 2015.