Simulação Leis de Newton

Um bloco de massa $m_{2}$ está sobre um plano inclinado com um ângulo de inclinação θ e está ligado por uma corda que passa sobre uma polia pequena a um segundo bloco suspenso de massa $m_{1}$ .

Há atrito entre o bloco $m_{2}$ e o plano inclinado e os coeficientes de atrito cinético e estático são $\mu _{c}$ e $\mu _{e}$ , respectivamente.

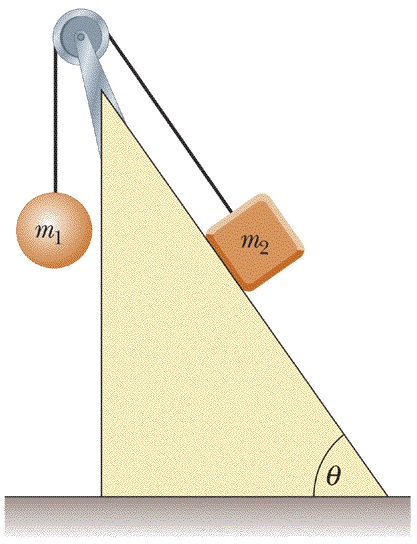
Caso – Considere que o bloco de massa $m_{2}$ está descendo o plano inclinado com aceleração igual a

a=g \left[ \frac{m_2(sen \theta-\mu_ccos \theta)-m_1}{m_1+m_2} \right]

e subindo o plano inclinado com aceleração

a=-g \left[ \frac{m_2(sen \theta+\mu_ccos \theta)-m_1}{m_1+m_2} \right]

Utilizando-se as definições abaixo

\begin{cases} m=\frac{m_1}{m_2} \\ cos^{2}\theta=1-sen^{2}\theta \end{cases}

mostre que a aceleração dos blocos é nula e os blocos ficam na iminência de se movimentarem, se os dois ângulos para os quais os blocos ficam no limite de subir ou de descer o plano inclinado forem dados por

sen\theta=\frac{m \pm \mu_e\sqrt{\mu_{e}^{2}-m^{2}+1}}{\mu_{e}^{2}+1}

Para que as raízes sejam sempre reais, tem-se que

m^{2} \leqslant \mu_{e}^{2}+1

Ou seja,

\begin{cases} m=0,6 \\ \mu_{e}=0,4 \end{cases}

tem-se que

\begin{cases} \theta_{1}=12,05° \\ \theta_{2}=55,66° \end{cases}

Crie uma aplicação, no Geogebra ou no AppInventor, que mostre esse comportamento.

(a) Solicite que o usuário forneça os valores das massas $m_{1}$ e $m_{2}$ ;

(b) Solicite que o usuário forneça os valores dos coeficientes de atrito cinético $\mu _{c}$ e coeficiente de atrito estático $\mu _{e}$ ;

(c) O programa deve informar ao usuário os valores dos dois ângulos limites $\theta_{1}$ e $\theta_{2}$ , para os quais os blocos permanecerão em repouso;

(d) O programa deve informar para o usuário a aceleração dos blocos nas condições tratadas acima;

(e) O programa deve informar quando as raízes não forem reais.

Bom trabalho!