Colisões – FIZIKO

Imaginemos o jogo de peteca, bolinha de gude, que utilizamos no início deste capítulo, consideremos que duas bolinhas colidam, podemos perguntar; o que acontece com as bolinhas após a colisão? Podemos ainda, fazer um estudo sobre a energia do sistema, e considerar casos particulares da colisão para saber se podemos comparar com os casos reais.

Entretanto, precisamos considerar alguns aspectos, sabemos, pela equação da velocidade do centro de massa de um sistema de partículas, que o momento linear do sistema de partículas, com massa total M = m₁ + m₂ + … + m_N, é igual ao momento linear do centro de massa do sistema

\vec{v}_{CM}=\frac{\displaystyle\sum_{i=1}^{N}m_{i}\vec{v}_{i}}{\displaystyle\sum_{i=1}^{N}m_{i}} \Rightarrow \vec{p}_{CM}=M\vec{v}_{CM}

Derivando-se a equação acima

M\frac{d\vec{v}_{CM}}{dt}=\frac{d\vec{p}_{CM}}{dt}=\sum_{i=1}^{N}\vec{F}_{ext,i}=M\vec{a}_{CM}

esta é a segunda lei de Newton para um sistema de partículas, que também é válida para um corpo rígido, como discutiremos mais adiante.

Tomando a colisão entre as duas bolinhas de gude, sabemos que as forças externas que atuam sobre as bolinhas são muito menores que a força impulsiva que age durante a colisão, de maneira que podemos desprezar a ação destas forças externas durante a colisão e, temos que o momento linear do sistema é constante no tempo, ou seja, o momento linear total do sistema deve ser conservado

\begin{cases} \displaystyle\sum_{i=1}^{N}\vec{F}_{ext}=0\\ \vec{p}_{total,f}=\vec{p}_{total,i} \end{cases}

apesar deste resultado valer sempre que a soma vetorial das forças externas se anularem, isso não basta para diferenciarmos os tipos de colisão.

Para as bolinhas de gude, uma parte da energia é transformada em vibrações e calor, no entanto, esse percentual é muito pequeno comparado à energia total do sistema, e durante a colisão, as bolinhas sofrem uma pequena deformação, semelhante ao que ocorre com uma mola, acumulando energia e, em seguida, liberando em forma de energia cinética. Como a energia de um sistema física é sempre conservada, podemos distinguir os tipos de colisões por meio do valor da energia cinética das partículas em colisão, assim, quando a energia cinética inicial total K_total,_i, for igual à energia cinética final total K_total,f, diremos que a colisão é elástica (K_total,f = K_total,i), caso contrário, teremos uma colisão inelástica (K_total,f $\neq$ K_total,i).

Dizemos que a colisão elástica é o caso ideal, pois só verificamos esta colisão em escala atômica, mas podemos considerar que este resultado vale para alguns casos do cotidiano, como uma boa aproximação.

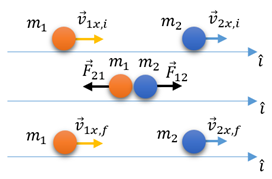
Colisão elástica entre duas partículas, indicando as velocidades iniciais e finais, com as forças internas newtonianas da colisão.

Consideremos o caso unidimensional, onde duas partículas com massas m₁ e m₂, movendo-se com velocidade $\vec{v}_{1,i} = v_{1x,i} \hat{i}$ e $\vec{v}_{2,i} = v_{2x,i} \hat{i}$ , respectivamente, como na figura acima. Após a colisão, as partículas assumem as velocidades finais $\vec{v}_{1,f} = v_{1x,f} \hat{i}$ e $\vec{v}_{2,f} = v_{2x,f} \hat{i}$ . Se considerarmos que houve uma colisão elástica, temos

\begin{cases} \vec{p}_{total,f} = \vec{p}_{total,i}\\ K_{total,f} = K_{total,i} \end{cases}

logo,

\begin{cases} m_{1}v_{1x,f} \hat{i} + m_{2}v_{2x,f} \hat{i} = m_{1}v_{1x,i} \hat{i} + m_{2}v_{2x,i} \hat{i}\\ \frac{1}{2}m_{1}v_{1x,f}^{2} + \frac{1}{2}m_{2}v_{2x,f}^{2} = \frac{1}{2}m_{1}v_{1x,i}^{2} + \frac{1}{2}m_{2}v_{2x,i}^{2} \end{cases}

reescrevendo.

\begin{cases} m_{1}(v_{1x,f} – v_{1x,i}) = m_{2}(v_{2x,f} – v_{2x,i} )\\ m_{1}(v_{1x,f}^{2} – v_{1x,i}^{2}) = m_{2}(v_{2x,f}^{2} – v_{2x,i}^{2}) \end{cases}

usando o resultado do produto da soma pela diferença

\begin{cases} m_{1}(v_{1x,f} – v_{1x,i}) = m_{2}(v_{2x,f} – v_{2x,i} )\\ m_{1}(v_{1x,f} + v_{1x,i})(v_{1x,f} – v_{1x,i}) = m_{2}(v_{2x,f} + v_{2x,i})(v_{2x,f} – v_{2x,i}) \end{cases}

combinando-as, temos

v_{1x,f} + v_{1x,i} = v_{2x,f} + v_{2x,i}

Esta equação é uma importante característica da colisão elástica unidimensional, com este resultado podemos verificar que a velocidade relativa entre as duas partículas se inverte em consequência da colisão. Podemos resolver o sistema

\begin{cases} m_{1}v_{1x,f} + m_{2}v_{2x,f} = m_{1}v_{1x,i} + m_{2}v_{2x,i} \\ v_{1x,f} + v_{1x,i} = v_{2x,f} + v_{2x,i} \end{cases}

Após alguns cálculos, obtemos

\begin{cases} v_{1x,f}=\left( \frac{m_{1}-m_{2}}{m_{1}+m_{2}} \right)v_{1x,i} + \left( \frac{2m_{2}}{m_{1}+m_{2}} \right)v_{2x,i}\\ v_{2x,f}=\left( \frac{2m_{1}}{m_{1}+m_{2}} \right)v_{1x,i} + \left( \frac{m_{2}-m_{1}}{m_{1}+m_{2}} \right)v_{2x,i} \end{cases}

Casos Particulares

(I) Consideremos que as massas são iguais, m₁ = m₂ = m,

\begin{cases} v_{1x,f}=v_{2x,i}\\ v_{2x,f}=v_{1x,i} \end{cases}

as partículas trocam suas velocidades e momentos lineares.

(II) Consideremos o alvo (m₂) em repouso (v_2x,i = 0),

\begin{cases} v_{1x,f}=\left( \frac{m_{1}-m_{2}}{m_{1}+m_{2}} \right)v_{1x,i} \\ v_{2x,f}=\left( \frac{2m_{1}}{m_{1}+m_{2}} \right)v_{1x,i} \end{cases}

podemos verificar que a partícula m₁ só modificará o sentido do movimento quando a massa m₂ for maior. Se tivermos, para este caso, m₁= m₂, vemos que a partícula m₁, após a colisão, ficará parada e a partícula m₂ se movimentará com a velocidade inicial de m₁. Tomemos m₂<< m₁, m₂ muito menor que m₁, então v_1x,f ≈ v_1x,i e v_2x,f ≈ 2v_1x,i, entretanto se m₂>> m₁, m₂ muito maior que m₁, então v_1x,f ≈ –v_1x,i e v_2x,f ≈ 0.

Colisão Completamente Inelástica Unidimensional

A colisão completamente inelástica tem como característica assumir o menor valor da energia cinética associada ao centro de massa. O centro de massa deve permanecer com um movimento retilíneo uniforme, assim o valor mínimo da energia cinética é o correspondente ao do centro de massa, levando-nos a observar que não deve haver movimentos internos relativos ao centro de massa após a colisão, logo, as partículas devem se movimentar juntas, coincidindo com o movimento do centro de massa e, como o momento linear total do sistema é conservado temos

v_{x,f}=\frac{m_{1}v_{1x,i} + m_{2}v_{2x,i}}{m_{1} + m_{2}}=v_{CM}

considerando que a partícula alvo esteja em movimento, conforme a situação da figura

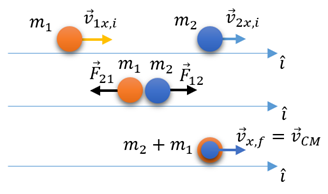
Colisão completamente inelástica entre duas partículas, indicando as velocidades iniciais e a velocidade final do centro de massa, com as forças internas newtonianas da colisão.

Podemos tratar as colisões inelásticas, chamadas também de colisões plásticas, aplicando o teorema do impulso e momento linear de uma partícula, aplicado aos impulsos de deformação e restituição, pois durante a colisão as partículas devem ser consideradas deformáveis e devem sofrer, por um curto período de tempo, a ação dessa deformação, até que atinjam uma deformação máxima, de modo que exerçam uma sobre a outra um impulso de deformação. Em seguida, ocorre um período de restituição, no qual as partículas retornam à sua forma original ou permanecem deformadas. O impulso de deformação é sempre maior que o impulso de restituição. O caso particular das colisões elásticas se explica pelo fato dos impulsos de deformação e restituição serem iguais e de sentidos opostos, assim,

\begin{cases} J_{D}=\int \vec{F}_{def}dt, \text{ impulso de deformação} \\ J_{R}=\int \vec{F}_{rest}dt, \text{ impulso de restituição} \end{cases}

Aplicando o teorema do impulso e momento linear às partículas, considerando que a velocidade das partículas em colisão durante a deformação máxima igual a v, e considerando o caso unidimensional, por motivos de simplificação, temos para a partícula m₁,

\begin{cases} J_{D} = m_{1}v + m_{1}v_{1x,i}\\ J_{R} = m_{1}v_{1x,f} – m_{1}v \end{cases}

e para m₂,

\begin{cases} J_{D} = m_{2}v + m_{2}v_{2x,i}\\ J_{R} = m_{2}v_{2x,f} – m_{2}v \end{cases}

tomando a razão $\frac{J_{R}}{J_{D}}$ , como sendo o coeficiente de restituição e, resulta

\begin{cases} e = \frac{v-v_{1x,f}}{v_{1x,i}-v}\\ e = \frac{v_{2x,f}-v}{v-v_{2x,i}} \end{cases}

combinando as equações e eliminando v, tem-se

e=\frac{v_{2x,f} – v_{1x,f}}{v_{1x,i} – v_{2x,i}}

podemos resolver simultaneamente as equações da conservação do momento linear e do coeficiente de restituição, o caso em que e = 1 é um caso particular em que já resolvemos acima, são as colisões elásticas.

Sabe-se, por meio experimental, que o coeficiente de restituição varia de forma apreciável com a velocidade de impacto, assim como com a forma e a dimensão dos corpos em colisão, desta forma, deve-se utilizá-lo quando este nos fornece resultados bons comparados aos experimentais.

O significado físico do coeficiente de restituição e, está no fato de que este quando assume os valores 0 e 1, representam os casos extremos da colisão

\begin{cases} e = 1, \text{ Colisão Elástica}\\ e = 0, \text{ Colisão Completamente Inelástica} \end{cases}

Colisão Bidimensional

Aplicaremos a teoria para o caso das colisões bidimensionais, que serão abordadas de forma simplificada, pois a partícula alvo estará inicialmente em repouso. Nada impede que tenhamos colisões elástica e inelásticas em sistemas de partículas em colisões, basta aplicarmos a teoria já abordada. Consideramos a figura abaixo que apresenta a partícula m₁, com velocidade $\vec{v}_{1}$ , colidindo com uma partícula alvo em repouso m₂.

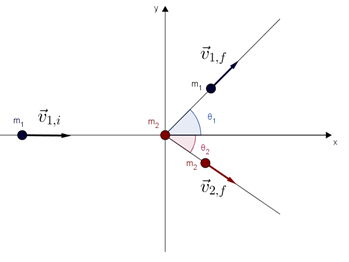
A partícula m₁ quando colide com a partícula m₂, em repouso, sofre um desvio θ₁ acima de sua direção de movimento, enquanto que, m₂ sofre um desvio θ₂ abaixo da direção do movimento inicial de m₁. Para uma colisão elástica, como já vimos

\begin{cases} \vec{p}_{total,f} = \vec{p}_{total,i}\\ K_{total,f} = K_{total,i} \end{cases}

o que nos dá, considerando as duas dimensões e que os vetores de base são $\left \{ \hat{i}, \hat{j} \right \}$ , cancelando o fator 1/2 da equação da energia cinética

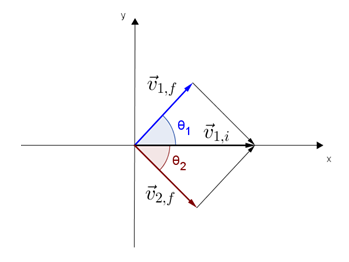
\begin{cases} m_{1}v_{1x,f}+m_{2}v_{2x,f}=m_{1}v_{1x,i}\\ m_{1}v_{1y,f}-m_{2}v_{2y,f}=0\\ m_{1}v_{1,f}^{2}+m_{2}v_{2,f}^{2}=m_{1}v_{1,i}^{2} \end{cases}

pela conservação do momento linear, podemos representar graficamente, a relação dos vetores momento linear final e inicial das partículas m₁ e m₂, como na figura a seguir

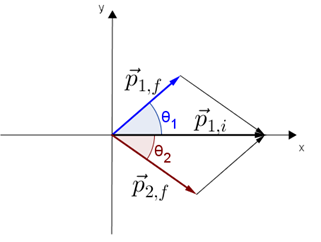
Relação vetorial dos momentos lineares inicial e final das partículas.

pela figura acima

\begin{cases} v_{1x,f}=v_{1,f} cos(\theta_{1})\\ v_{1y,f}=v_{1,f} sen(\theta_{1})\\ v_{2x,f}=v_{2,f} cos(\theta_{2})\\ v_{2y,f}=v_{2,f} sen(\theta_{2}) \end{cases}

Para o caso particular onde m₁ é igual a m₂, temos

\begin{cases} v_{1x,f}+v_{2x,f}=v_{1x,i}\\ v_{1y,f}=v_{2y,f}\\ v_{1,f}^{2}+v_{2,f}^{2}=v_{1,i}^{2} \end{cases}

este resultado pode ser representado graficamente, tomando-se o comportamento dos vetores velocidades e observando que a equação que relaciona as velocidades quadráticas são as escrita acima, verifica-se o comportamento típico do teorema de Pitágoras, permitindo-nos concluir que a soma dos ângulos de espalhamento das partículas obedece a relação $\theta_{1}+\theta_{2}=90^0$ .

Gráfico com a representação vetorial das velocidades das partículas.

REFERÊNCIAS

HIBBELER, R. C. Dinâmica: Mecânica para Engenharia. Edição: 12 ed. São Paulo (SP): Pearson Universidades, 2010.

NUSSENZVEIG, H. M. Curso de Física Básica: Mecânica. Edição: 5 ed. São Paulo – SP: Blucher, 2013.

PEDUZZI, L. O. Q.; PEDUZZI, S. S. Física Básica B. 2^a ed. Florianópolis – SC: Universidade Federal de Santa Catarina/CFM/CED/UFSC, 2010.

RESNICK, R.; WALKER, J.; HALLIDAY, D. Fundamentos de Física – Volume 1 – Mecânica. Edição: 10 ed. Rio de Janeiro – RJ: LTC, 2016.

SERWAY, R.; JEWETT, J. Princípios de física – vol. I: Volume 1. Edição: 2 ed. São Paulo-SP. Cengage Learning, 2014.

YOUNG, H. D.; FREEDMAN, R. A. Física de Sears & Zemansky: Volume I: Mecânica: Volume 1. Edição: 14 ed. São Paulo – SP: Pearson Universidades, 2015.