OSCILAÇÕES

OSCILAÇÕES SIMPLES

Uma função f:ℝ→ℝ é dita periódica de período T (também chamada de T-periódica) se existe uma constante positiva T tal que

f(t) = f(t+T)

para todo t ∈ ℝ.

Algumas funções periódicas admitem um menor período, chamado de período fundamental. A frequência fundamental é então dada por f=1/T e a frequência angular fundamental é dada por w_f = 2πf.

Oscilador Massa-Mola

Utilizando-se a segunda Lei de Newton e analisando as força que atuam no corpo de massa m, podemos verificar que há sobre a massa uma força peso P, uma força elástica F_el, a força normal N e sem força de atrito entre o bloco e a superfície.

logo, aplicando a Segunda Lei de Newton

\vec{F}_{R} = m \vec{a} \\
\vec{F}_{el} + \vec{P} + \vec{N} = m \vec{a} \\

como a força peso P é igual a força normal N

\vec{F}_{el} = m \vec{a}

considerando o movimento em uma dimensão 1D, tem-se

-kx = m \frac{d^2x}{dt^2} \\
\frac{d^2x}{dt^2} + \frac{k}{m} x = 0

a equação acima é chamada de equação de movimento do oscilador harmônico simples OHS, defini-se a frequência angulardo oscilador massa-mola por

\omega^2=\frac{k}{m}

portanto, pode-se escrever que

\frac{d^2x}{dt^2} + \omega^2 x = 0

Uma possível solução para a equação de movimento do OHS é a função

x(t) = A \cos (\omega t + \theta_{0})

Faça a prova!

Pode-se determinar a velocidade e a aceleração do OHS, logo

v_{x} = \frac{dx}{dt} = -A \omega \sin(\omega t + \theta_{0}) \\
v_{x,max} = A \omega

a_{x} = \frac{dv_{x}}{dt} = -A\omega^2 \cos(\omega t + \theta_{0})\\
a_{x,max} = A \omega^2

Obtendo relações entre as grandezas

\sin^2 \theta +\cos^2 \theta = 1  \\
\left(-\frac{v_{x}}{A \omega}\right)^2 + \left(\frac{x}{A}\right)^2 = 1 \\

\left(\frac{v_{x}}{ \omega}\right)^2 + x^2 = A^2

e

\sin^2 \theta +\cos^2 \theta = 1  \\
\left(-\frac{v_{x}}{A \omega}\right)^2 + \left(-\frac{a_{x}}{A\omega^2}\right)^2 = 1 \\

v_{x}^{2} + \left(\frac{a_{x}}{\omega}\right)^2 = A^2 \omega^2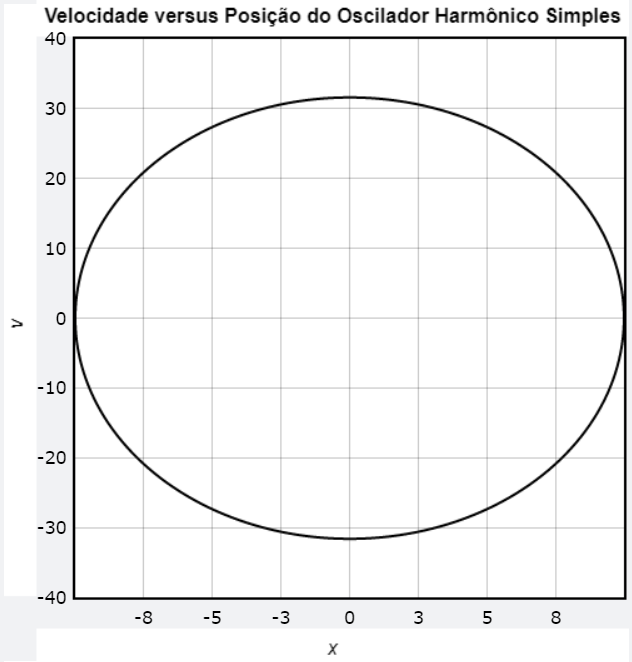

Energia no OHS

A energia cinética de um corpo em movimento é determinada pela expressão

E_{C} = \frac{1}{2}mv^2

Como vimos acima, a velocidade de um oscilador harmônico varia com o tempo e é descreita por uma função periódica, logo

E_{C} = \frac{1}{2} m \left[-A \omega \sin (\omega t + \theta_{0}) \right]^2 \\ ou \\
E_{C} = \frac{1}{2} m A^2 \omega^2 \sin^2 (\omega t + \theta_{0})

A energia potencial no sistema massa-mola é elástica, portanto

U = \frac{1}{2} k x^2 

Como sabemos, a posição de um oscilador harmônico varia com o tempo e é uma função periódica, assim

U = \frac{1}{2} k \left[ A \cos (\omega t + \theta_{0}) \right]^2 \\
ou
\\
U = \frac{1}{2} k A^2 \cos^2 (\omega t + \theta_{0})

A energia mcânica ao contrário do que se espera não varia com o tempo, mantendo-se constante, dada por

E = E_{C} + U

E =  \frac{1}{2} m A^2 \omega^2 \sin^2 (\omega t + \theta_{0}) + \frac{1}{2} k A^2 \cos^2 (\omega t + \theta_{0})

Se utilizarmos a expressão,

\omega^2 m=k 

logo,

E = \frac{1}{2} A^2k \sin^2(\omega t + \theta_{0}) + \frac{1}{2} A^2 k \cos^2(\omega t + \theta_{0}) 

Utilizando-se

\sin^2 \theta + \cos^2 \theta = 1

temos,

E = \frac{1}{2} kA^2 = \frac{1}{2}mA^2 \omega^2

OSCILAÇÕES AMORTECIDAS

Chamamos de amortecimento a diminuição da amplitude provocada por uma força dissipativa e de oscilação amortecida o movimento correspondente.

Se considerarmos o sistema massa-mola submetido a uma força dissipativa proporcional à velocidade, do tipo

\vec{F}_{d} = -b\vec{v} 

A equação de movimento para este oscilador dependerá da força elástica e da força dissipativa

\vec{F}_{R} = \vec{F}_{el} + \vec{P} + \vec{N} + \vec{F}_{d} = m\vec{a}

como a força peso se anula com a força normal, tomando-se o sistema oscilando ao longo do eixo x, em movimento 1D, tem-se

-kx-bv_{x}=m\frac{d^2x}{dt^2}

Reescrevendo a equação acima,

\frac{d^2x}{dt^2} + \frac{b}{m}\frac{dx}{dt} + \frac{k}{m}x = 0

Uma boa prática é definirmos o operador matemático

D = \frac{d}{dt} \\
\text{e} \\
D^2 = \frac{d^2}{dt^2}

pode-se escrever a equação de movimento na forma

D^2x + \frac{b}{m}Dx + \frac{k}{m}x = 0 \\
\text{logo,} \\
\left(D^2 + \frac{b}{m}D + \frac{k}{m}\right)x = 0

Resolvendo a equação do segundo grau dentro dos parenteses, temos

D = - \frac{b}{2m} \pm \sqrt{\left( \frac{b}{2m}\right)^2-\frac{k}{m}}

O termo da frequência pura do oscilador ω₀, sem a influência do amortecimento é predominante, e dado por

\omega_{0}^2 = \frac{k}{m} 

Ajustando a equação de D, teremos

D = -\frac{b}{2m} \pm \sqrt{-1}\sqrt{\omega_{0}^2 - \left(\frac{b}{2m}\right)^2}

com

i = \sqrt{-1}

A equação acima apresenta dois valores para D, o que nos sugere que uma possível solução é uma combinação linear de exponenciais complexas de t, assim,

x(t) = C_{1}\exp(D_{1}t) + C_{2}\exp(D_{2}t)

teremos,

x(t) = C_{1}\exp{\left[t \left( -\frac{b}{2m}+i\sqrt{\omega_{0}^2-\left( \frac{b}{2m}  \right)^2} \right) \right]} + \\ +C_{2}\exp{\left[t \left( -\frac{b}{2m}-i\sqrt{\omega_{0}^2-\left( \frac{b}{2m}  \right)^2} \right) \right]}

Utilizando-se a condição de que,

C_{1} = C_{2} = \frac{A}{2}

podemos reescrever a equação acima como,

x(t) = \frac{A}{2} \exp{\left( -\frac{b}{2m}t\right)} \exp{\left[t \left( +i\sqrt{\omega_{0}^2-\left( \frac{b}{2m}  \right)^2} \right) \right]} + \\ +\frac{A}{2} \exp{\left( \frac{b}{2m}t\right)} \exp{\left[t \left( -i\sqrt{\omega_{0}^2-\left( \frac{b}{2m}  \right)^2} \right) \right]}

simplificando,

x(t) = \frac{A}{2} \exp{\left( -\frac{b}{2m}t \right)} \left\{ \exp{(+it\omega')} + \exp{(-it\omega')} \right\}

onde ω’ é a frequência angular do oscilador amortecido, dada por

\omega' = \sqrt{\omega_{0}^2 - \left(\frac{b}{2m}\right)^2}

Utilizando a identidade

\cos{z} = \frac{e^{iz}+e^{-iz}}{2}

Logo, acrescentando a influência da constante de fase θ₀

x(t) = \displaystyle{A e^{-\frac{b}{2m}t}\cos{(\omega' t + \theta_{0})}}

A equação acima é a uma solução da equação de movimento do Oscilador Amortecido, deixaremos que o estudante tire a prova.

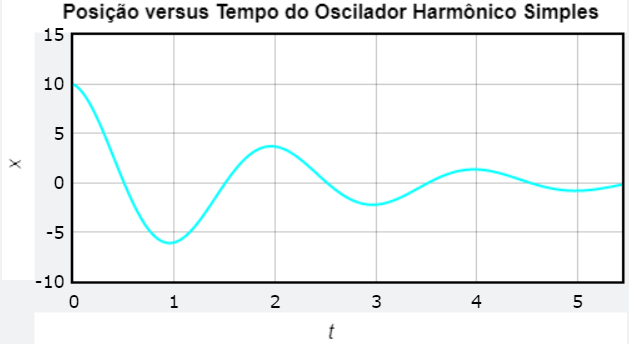
Podemos realizar o estudo da frequência do oscilador amortecido, vemos que quando o valor de b é menor que o valor crítico, que é

\text{se }\omega' \rightarrow 0 \text{, temos que, } \frac{k}{m} - \frac{b^2}{4m^2} = 0

e o valor crítico de b é dado por

b = 2\sqrt{km}

Na condição acima de b, tem-se um amortecimento crítico.

Para b menor que o valor crítico, a condição denomina-se subamortecimento.

A condição onde b é maior que o valor crítico corresponde ao superamortecimento.

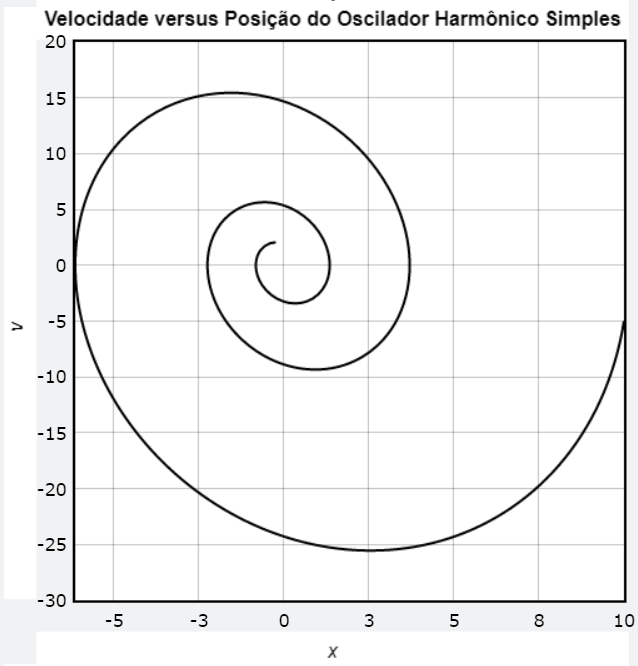
Nas oscilações amortecidas, a força do amortecimento não é conservativa; a energia mecânica do sistema não é constante e diminui continuamente, tendendo a zero depois de um longo tempo.

A taxa de variação da energia pode ser calculada utilizando-se

\frac{dE}{dt} = \frac{dE_{C}}{dt} + \frac{dU_{el}}{dt}

as derivadas são

\frac{dE}{dt} = \frac{1}{2}m \left(2v \frac{dv}{dt}\right) + \frac{1}{2}k \left(2x\frac{dx}{dt} \right)

simplificando

\frac{dE}{dt} = v \left( m \frac{dv}{dt} + kx\right)

o termo dentro dos parenteses é obtido pela equação de movimento, logo

m \frac{dv}{dt} + kx = -bv

assim,

\frac{dE}{dt} = -bv^2

A equação acima informa que, a taxa de variação da energia mecânica total é igual ao negativo da taxa com a qual a força do amortecimento realiza trabalho sobre o sistema.

PÊNDULO SIMPLES

O pêndulo smples é um modelo físico ideal, leva em consideração o comportamento de uma partícula de massa m presa em um fio de comprimento L com massa desprezível e inextensível, com a outra extremidade do fio presa em um ponto fixo.

A partícula é levemente puxada para a lateral, produzindo um deslocamento angular θ, removendo-a de seu estado de equilíbrio. Neste ponto, a força peso atua como uma força restauradora, fanzendo a partícula retornar ao seu ponto de equilíbrio, desprezando-se a força de arrasto do ar, a energia inicial imprimida ao pêndulo é conservada fazendo com que a partícula execute um movimento periódico, ver figura.

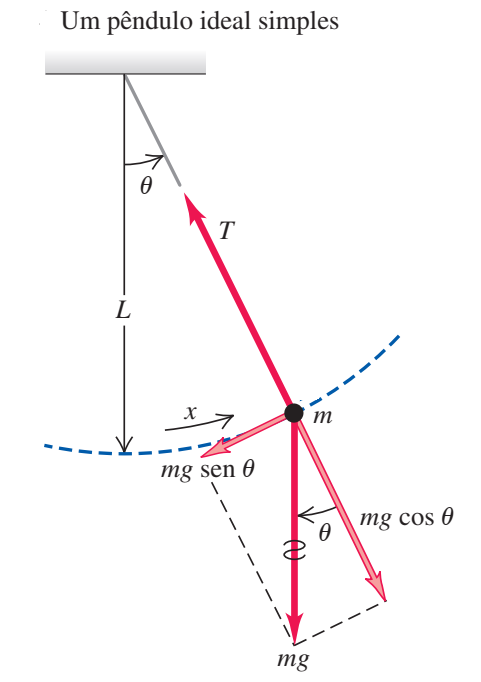
Como vemos na figura, a partícula executa ummovimento circular de raio L, desta maneira podemos escrever que o valor de x é dado por

x = \theta L

A componente tangencial do peso é a força restauradora, portanto

F_{t}=-mg\sin{\theta}

Destaca-se ainda, a força tangencial como sendo o produto da massa da partícula por sua aceleração tangencial a_t dada por

\displaystyle{F_{t}=ma_{t}}\\
.
\\
\displaystyle{a_{t}=\frac{d^2x}{dt^2} }\\  
.  \\
\displaystyle{a_{t}=L \frac{d^2 \theta}{dt^2}}

A equação de movimento do pêndulo simples é dada por

mL \frac{d^2\theta}{dt^2}+mg\sin{\theta}=0 \\
. \\
\frac{d^2 \theta}{dt^2}+\left(\frac{g}{L}\right)\sin{\theta}=0

A equação de movimento acima é não-linear e não se caracteriza como um oscilador harmônico simples, no entanto, se utilizarmos o resultado para pequenos ângulos sen(θ) ≈ θ , a equação passa ter as mesmas características do oscilador simples

\frac{d^2 \theta}{dt^2}+\left(\frac{g}{L}\right)\theta=0

Temos, como resultado para a frequência angular ω, quando θ for muito pequeno, a expressão

\omega^2 = \frac{g}{L}

Logo, o período será

T = 2 \pi \sqrt{\frac{L}{g}}

Note que o período das pequenas oscilações não dependa da massa m da partícula.

OSCILAÇÕES FORÇADAS

OSCILAÇÃO FÍSICA

BIBLIOGRAFIA

• RESNICK, Robert, HALLIDAY, David & WALKER, Jearl. FUNDAMENTOS DE FÍSICA: Gravitação, Ondas e Termodinâmica, Volume 2, 6^a Edição. Rio de Janeiro: LTC, 2002.
• NUSSENZVEIG, H.M. – CURSO DE FÍSICA BÁSICA, VOL 2, ED. EDGARD BLÜCHER LTDA.
• SERWAY, Raymond A., & JEWETT Jr, John W. PRINCÍPIOS DE FÍSICA: Movimento Ondulatório e Termodinâmica, Volume 2, 3ª Edição. São Paulo: Cengage Learning, 2008.
• TIPLER, Paul A. & MOSCA, Gene. FÍSICA: Mecânica, Oscilações e Ondas, Termodinâmica, Volume 1, 5ª Edição. Rio de Janeiro: LTC, 2006.
• SEARS, Francis W. & ZEMANSKY, Mark W.; YOUNG, Hugh D. & FREEDMAN, Roger A. FÍSICA II: Termodinâmica e Ondas, 12ª Edição.  São Paulo: Pearson Education.